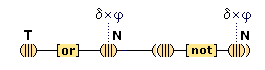A Neo-Traditional View of Concepts and Meaning
Associate Professor of Philosophy
Loyola University Chicago
Abstract: This article provides a neurological analysis of the different kinds of connections that exist among the items that constitute our active thoughts. The analysis is based throughout on the premise that our thoughts are brought about by the activations of dedicated neuron groups. By this analysis we are able to clarify simple puzzles about thinking, display how sensory perception, memory, and language are related to concepts, explicate the nature of simple and complex concepts and conceptual representations, and demonstrate the extemporaneous structure of our propositional thoughts, together with the dynamic conditions that form their constitution.
For a printable, non-animated, PDF version of this article, click here
Copyright © 09/2000, 05/2003, 1/2008, 1/2009. All rights reserved. This article is the intellectual property of the author. No part of this article may be reproduced or distributed in any form without the author's written permission, except that the reader is allowed to download this article and print one copy for the sole purpose of studying it.
PART I. BASIC COGNITIVE UNITS
| §00. Introduction | 1 |
| §01. Representations and cognitive structures | 1 |
| §02. Connections among neural nodes | 4 |
| §03. Recognition as an indicator of concepts | 6 |
| §04. Cognitive adjunction | 6 |
| §05. Specific and non-specific sensory perception | 7 |
| §06. Individuative connection | 8 |
| §07. Feature unit connection | 9 |
| §08. Simple concept connection | 11 |
| §09. Simple verbal connection | 12 |
| §10. Undenominated concepts | 14 |
| §11. Feature units as the basic units of meaning | 15 |
PART II. COMPLEX CONCEPTS
| §12. Simple and complex concepts | 20 |
| §13. Analytic connection | 22 |
| §14. The non-existence of disjunctive concepts | 23 |
| §15. Quasi-concepts | 25 |
| §16. Family resemblance accounts of concept meaning | 26 |
| §17. Relational concepts | 30 |
| §18. Transferred Adjunction | 32 |
| §19. Strong connection | 32 |
| §20. Iconic memory connection | 36 |
| §21. The weakness of strong connection | 37 |
| §22. Extemporaneous conceptualizations | 40 |
PART III. PROPOSITIONAL THOUGHTS
| §23. Propositional adjunction | 41 |
| §24. Combinatorial conceptual structures | 43 |
| §25. Predication structures | 45 |
| §26. Evaluating simple predications | 49 |
| §27. Evaluating quantified predications | 55 |
| §28. Compound propositions | 62 |
| §29. Conformity with standard logical inferences | 68 |
| §30. Experimental results | 73 |
| §31. Conclusion of this paper | 73 |
§0. Introduction.
Contemporary philosophy has for some time identified the troublesome traditional notions of having a concept, or entertaining a proposition, with the notion of having a disposition to behave and use language appropriately in given circumstances. But despite valuable analytical benefits, dispositional theories of thought have lacked a satisfactory explanation of how dispositions themselves are to be understood. In virtue of what do speakers of a language have the mind-boggling dispositions to use the words of the language appropriately? This is a mystery far greater than the mystery attending the traditional notions of concept and proposition.
In recent years cognitive science has begun to provide such an explanation. The human cognitive system is a structured system of causally interconnected cognitive nodes whose activations bring about the activity of thought. The traditional notions of concept, proposition, and meaning, as well as language dispositions, seem capable of having a place within such a connectionist framework, though only detailed empirical and theoretical studies can determine whether, and to what the extent, this is so. Our purpose is to promote this kind of study of philosophical cognitive issues. Throughout we will make number of explanatory proposals, but often while making philosophical proposals that are themselves rather contentious, for example, proposals about the nature of language, of perception, of memory, and of conceptual thought. This is an acknowledged difficulty, but our purpose is not to either support or criticize plausible philosophical views. And on the other hand, we make some speculative, theoretical proposals about the possible ways in which neuronal activity is related to human thought, but without the kind of empirical support that is required for scientific hypotheses. This is also an acknowledged difficulty, but one for which there is no present help, since the state of empirical knowledge regarding such matters is extremely limited. Our purpose, then, is to present a theoretical framework in which some traditional notions in epistemology and the philosophy of mind are explicated through some contemporary notions in cognitive science. We hope in this way to create an interface in which each field of study is put in the service of the other.
§1. Representations and cognitive structures.
We assume that our minds are cognitive systems. Such systems are composed of various parts that at various times have a certain activity. Consequently, such systems are characterized by sequences of the activities of its parts. What makes our minds special is that such sequences have special arrangements, as we shall see. We designate these arranged sequences of activities as the cognitive processes of the system. We also assume that the commonsense processes that we are introspectively aware of consist in their entirety of, and are brought about by, such systemic cognitive processes. That is, when we think, see, hear, feel, remember, speak, calculate, hope, and so on, we are engaged in such systemic cognitive processes.
We propose that activity within our cognitive systems be understood as follows. As we shall explain below, when certain parts, that we designate as cognitive nodes, become active in their basic characteristic manner, they not only cause other such parts to become active in like manner, but they also bring about a special type of activity at a different level of organization within the system. We designate all such secondary activities to be cognitive representations, and we correspondingly propose that our individual active thoughts are to be construed as such cognitive representations. Thus, the sights that we see, the word that we hear, the pains that we feel, the scenes that we remember, the numbers that we calculate, the ideas that we relate, the hopes that we have, they are all individual cognitive representations within our cognitive systems.
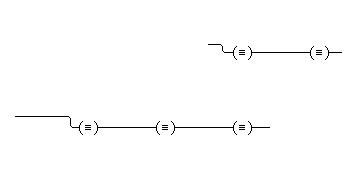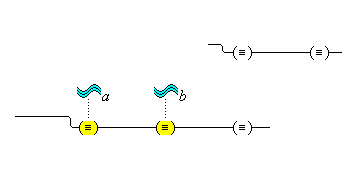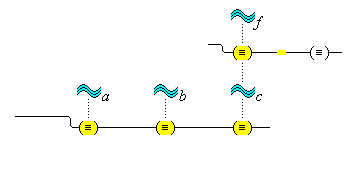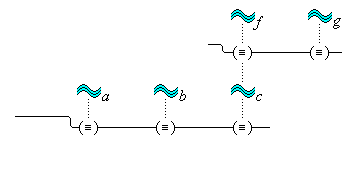
Our active thoughts (in the broad sense), therefore, are cognitive representations and are brought about by the activation of certain individual cognitive nodes (i.e., structures, or units) that are fixed parts of the cognitive system. We suppose that cognitive representations are patterned activities brought about by the activation of these structures much in the same way as, when a tuning fork is struck, the fork begins to vibrate, and a wave pattern is formed, or when a pebble drops in water, the water becomes active, and a rippled wave pattern in the water is formed. So, there are certain structured parts of the cognitive system such that, when they are activated, the cognitive system begins activities whose spans are cognitive representations. When a certain part of the auditory sensorium is activated, the cognitive system is thus active and hears the sound "apple," and when a certain conceptual unit is activated, the cognitive system is thus active and thinks the concept (elephant), producing a certain understanding in this way. Figure 1 illustrates the relationship between fixed cognitive structures, their activations, and the resulting cognitive representations.
We also make the more specific empirical assumption that the cognitive structures to which we have been referring are structures of neurons in the brain, and that the activations of these neural structures bring about activities, which in some cases is the thinking of conceptual thoughts, in others the seeing of a scene, in others the feeling of warmth, and so on.(1) With this assumption, our account is subject to the empirical constraints provided by neuroscience.
One empirical constraint is the now commonly accepted view that our thought processes occur in parallel and are distributed in the sense that they involve many neurons perhaps widely distributed over diverse areas of the brain. Concomitantly, we assume that individual cognitive structures are, likewise, distributed structures. So, we will not assume that there are individual neurons for the concepts (grandmother), (hamburger), and (the Moon), such that if those neurons were destroyed, we would no longer be able to think those thoughts. Rather, we will assume that cognitive structures are distributed neuron groups. On the other hand, a group of neurons, of considerable size and distribution, with special organization, depending on its synaptic connections, can nevertheless behave as a unit, and can therefore be taken to be a discrete, functional unit within the cognitive system. We will not dwell on the question as to what extent and in what ways cognitive structures are neuron groups. We will simply refer to whatever neural structures there are as neural nodes. Our analysis will thus proceed on the assumption that the discrete cognitive structures of the cognitive system are neural nodes in the sense here described. In what follows, we will use the terms structures, units, and nodes interchangeably.(2)
We pause to note that the account we are presenting weaves together three different explanatory frameworks: (1) a given framework about our commonsense understanding of cognitive processes, a folk psychology, as it is sometimes called, and something we take to be more or less correct; (2) a given framework of neuroscience that centers on the nature and activity of neurons, about which a great deal is known, but about which very little is known regarding the mechanics of how people think; and (3) what is our purpose to present, a more abstract and theoretical explanatory framework of systems, parts, connections, activations, processes, forms, storage, retrieval, and what not, that tries to incorporate and accommodate the other two frameworks.
The cognitive structures and representations that we postulate are:
| (momentary) cognitive representations (1) sensory representations (2) iconic memory representations (3) feature representations (4) formal representations (5) conceptual representations (6) conceptual memory representations (7) propositional representations |
(permanent) cognitive structures sensorial structures iconic memory units feature units formal nodes conceptual nodes conceptual memory nodes predication structures |
(1) sensory representations, which constitute our present sensory awareness of a qualitatively featured environment; and the sensory cognitive structures, (the parts of the various sensoriums: the visual cortex, the auditory cortex, etc.), whose activations bring these representations about;
(2) iconic memory representations, that partially reproduce in some way our previous sensory experience, and that are brought about by the activation of corresponding iconic memory units;
(3) feature representations, of the individual sensory, spatial, or kinematic qualities of our experience; that are brought about by the activation of corresponding feature units, that we suppose are the basic units of meaning that define our simple thoughts;
(4) formal representations, that are brought about by the activation of formal cognitive nodes,
(5) conceptual representations, the conceptual thoughts we engage in; that are brought about by the activation of single conceptual nodes, (either concepts or quasi-concepts), or by a sequence of extemporaneously linked conceptual nodes. Conceptual nodes function as relay-points in a network of interconnected cognitive nodes, to hierarchically organize all the information (both incoming and stored) that is available in the cognitive system;
(6) conceptual memory representations, that partially reproduce in some way episodes of previous conceptual thoughts and that often accompany our iconic memories, and that are brought about by the activation of corresponding conceptual memory units.
(7) propositional representations, the structured conceptual thoughts we have, that we sometimes express in sentences, and that are brought about by the activation of predication structures, that have a connection to concepts and formal cognitive nodes.
All these structures and representations will be introduced and discussed in ample detail below.
We suppose, then, that all cognitive structures are individual neural nodes, that have spatial, temporal, and causal properties in virtue of their neuronal substructure. We also suppose that these structures are connected in some fashion to other cognitive structures, and that they come to be activated under certain conditions. Throughout we make use of the important fact that the activation of nodes is transmitted along the nodes of a connected path. Our thought processes, consequently, are activities brought about by sequences of such activations. While the mind has many dispositions and abilities of action and speech, all such dispositions are necessarily derivative and are generated by the systematic arrangement of the cognitive structures of the mind. (Explanatory appeals to dispositions must therefore be second-best.) Cognitive nodes are quasi-permanent fixtures of the cognitive system, once they exist. By contrast, cognitive representations exist only for as long as the cognitive nodes are activated.
§2. Connections among neural nodes.
It is important that the notions of connection and activation be properly understood. Neural nodes are distributed neuron groups. So, while there are the lower level connections and activations among individual neurons, we will be concerned only with connections and activations that exist among distributed neuron groups. (It is an empirical question how such group connections are arranged and in what manner group activations come about, and time will tell the story.) In a general sense, a connection is simply a causal relation in which the activation of one node causally brings about the activation of another one. This general sense is sufficient for many of the distinctions we will make. But sometimes a more particular understanding is required. We call a connection between two neural nodes a brute synaptic connection if the aggregate of the individual synaptic connections that exist between the individual neurons of the nodes is sufficient to constitute a causal activation relation between them. In such cases, brute activation is the proposed mechanism whereby one nodes activates a connected node. We assume that such activation mirrors the activations that occur at the lower neuronal level: there is a transmission of some sort of impulse, and if the transmitted amount sufficiently exceeds the activation threshold of the connected node, the connected node will be successfully activated. One can picturesquely describe this brutal situation as one in which one node is active by "humming its tune" and then "kicking" a connected node; whereupon the second node responds by "humming its tune" and "kicking" some further connected node, and so on. Part of the idea of brute activation is that a given transmission may not be strong enough to activate a connected node. In such a case, the connected node will not be activated, unless some other nodes provide additional transmissions sufficient to activate the connected node. Neuroscientific theories commonly propose a mechanism of brute activation. We have more to say about brute synaptic activation in section 21 below.
The view that we take regarding the constitution of our active thoughts enables us to distinguish a second type of nodal connection and activation. Since our thoughts are distinct and have a certain constant character (as revealed in introspection), we will suppose, first, that each cognitive neural node has a unique, natural, characteristic activation pattern, that derives from both the arrangement and the characteristic spiking frequencies of the individual neurons inside the node.(3) If this is so, then we may conclude that the activation of a cognitive node produces a corresponding unique, characteristic activation wave pattern. And, we take it that such propagated wave patterns constitute, that is, are, the active thoughts we have.
Again, if all this is so, then we can speculate that these activation wave patterns, and thus our thoughts, are similar in some ways to other wave patterns, such as the standard complex waves patterns of sound and light. Two important physical laws are then available to us. The first is a resonance principle. When a given source propagates a wave with a given frequency, all structures that are inherently capable of vibrating at that frequency will begin to vibrate at that frequency, that is, will begin to resonate with the wave, when they are subjected to the wave. The importance of resonance is that when a neural node is brought into resonance with the activation wave pattern of another node in virtue of the natural patterns they both have, the relation between the two simply is a causal activation relation, and it must thus be considered a connection among the nodes. Accordingly, we are able to distinguish resonance connections and activations from synaptic connections and brute activations. We may picturesquely describe a case of resonance activation as one in which one active node "hums its tune," and elsewhere certain other nodes respond, "Oh, I know that one. I'll just hum along."
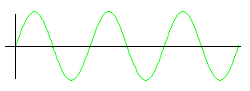
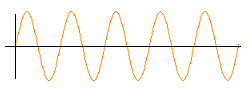
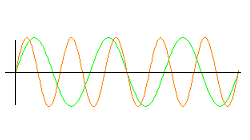
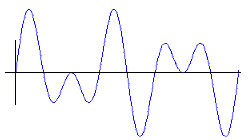
The second physical law available to us is the superposition principle that states that a complex wave pattern resulting from the superposition of other waves patterns preserves the physical characteristics of the component wave patterns. This would apply to the activation wave patterns of neural nodes as well. When the activation wave patterns of different neural nodes are superimposed, their combined activation wave pattern preserves the characteristics of the component wave patterns. This would yield the very important and very intuitively satisfying result that when different thoughts are combined into a single complex thought, the resultant thought preserves the characteristics of the component thoughts.(4) For example, the single wave pattern that is the single thought (Rembrandt painted the Night Watch) contains as isolatable components the several wave patterns that are the individual thoughts (Rembrandt), (painted), and (the Night Watch).
| The superposition of sound waves preserves the identity of the component waves | ||
 |
 |
|
 |
 |
|
 |
 |
|
| These two waves are the same | ||
 |
 |
|
We should note that the kind of activation patterns we are discussing is considerably different from the kind of activation patterns that are usually proposed in Connectionist models. In those theories, each node does not have an inherent activation pattern, but is rather associated with a numerical weight value that is the sum all the weights of the nodes that are connected to it. In Connectionist theories the activation pattern of a given node is the distributed network of the weights of all the nodes that are connected to it.(5) The Connectionist notion of distributed networks and associated activation patterns has had some success in computer simulations of simple sensory feature detection, but no Connectionist models exist that simulate full-blown conceptual thought. Still, we are able to make use of the Connectionist notion of activation pattern in our later discussion of strong and weak connections, though we will more generally think of such activation patterns as global activation contexts that can affect some activations.
§3. Recognition as an indicator of concepts.
Concepts play a dominant role in our thought processes. Almost all our thoughts engage concepts, while the other kinds of cognitive structures are active only in select circumstances that evoke them. But introspection reveals a problem regarding concepts. We are conscious only of our sensory experience (the words we hear, the sights we see, the feelings we have, and so on), and we never seem to have an awareness of anything conceptual in nature.
So, it is appropriate to consider by what criteria we can gauge the presence of concepts in our mental life. Certainly, our spoken words are indicators of a large store of concepts, and from this point of view, we can get some account of what our concepts are. But, if we take only our words as signs of our concepts, we will neglect the greater part of what we are able to conceive, since undenominated concepts far outnumber denominated ones, as we will discuss in section 10 below. We propose instead the following criterion:
representation, and is thus brought about by the activation of corresponding concepts.
We do not require here that the recognition at issue be correct or appropriate, but only that the recognition occurs. We take a recognition to be some kind of familiarity with something, and we take every inkling of familiarity to be an indication that some concept is being thought. As we look casually at a scene before us, the elements of the scene appear normal, as they usually do, and we pass over them without special consideration. Things seems familiar, at least to the extent that we are not puzzled by them — until our eye catches something, and we dwell on it a bit longer, only to have it fade into a comfortable familiarity, or occasionally, an uncomfortable (huh?). In other words, as we look casually at a scene before us, a multitude of conceptual representations come into being, as conceptual structures are activated, on account of which the items before us are familiar: understood and recognized. When we focus on things, the processes of understanding them becomes more complicated, involving a number of different kinds of structures, connections, and representations.(6)
§4. Cognitive adjunction.
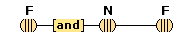
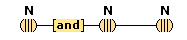
There is a situation that occurs when we perceive or think, a situation in which one perception or thought leads to some other thought. We call this situation cognitive adjunction, and where concepts are involved, conceptual adjunction. In simple cases, this situation consists of two concurrent cognitive representations that are respectively brought about by the activations of two cognitive nodes that are connected, in the sense that the activation of the one node causes the activation of the other. We see a red apple, and then we also think (red); or we think (snow) and then we also think (cold). We have here a causal sequence that begins with the activation of a cognitive node X and then continues with the additional, concurrent activation of a cognitive node Y, where each activation brings about a corresponding representation, so that there is an adjunction of two concurrent, active thoughts. After some interval the activations cease, and the adjunction of the corresponding representations fades and terminates. Cognitive adjunctions are typically more wide-ranging than the simple case just described. Since causal activations usually continue along a connected path, and since nodes are typically directly connected to more than one node, cognitive adjunctions typically involve the activations of a number of nodes X1, . . . , Xn, activations that all have a common causal origin. It will become apparent later that cognitive adjunctions are mostly conceptual ones, in as much as when sensory, iconic, feature, conceptual, or linguistic representations are adjoined, concepts are usually involved.(7)
We assume that our mental activities form a stream of cognitive adjunctions. This stream is not continuous, but constantly renewed with new starts. Many of our mental activities are continued through adjunction, up to a point, and many are likewise stopped short by some new distraction, that drives the stream in another direction. Clear examples of cognitive adjunction are easy to find. We see a red apple, and then think of it as (red), as (apple), and as (food), recognizing it in those ways. And in a different way, we can hear the sound "red" and think its meaning (red).
Concurrence is necessary for adjunction, but it is not sufficient, since many representations are concurrent that do not involve cognitive adjunction, as we can ascertain from introspection. Easy cases that come to mind are those occasioned by diverse sensory experiences, such as when we have the thoughts (bird) and (tree), when we hear some sound while we are seeing some view. Here, the following are concurrent and adjoined: we hear the sound, we think (bird); as are the following: we see the scene, we think (tree). But we do not consider the four thoughts together, because there is no causal link between all four of those thoughts. In the same way, when someone says the word "cat" very loudly, the thoughts (very loud) and (cat) are concurrent, but they are not conceptually adjoined, for otherwise we would be thinking (very loud cat), which is quite a different thing.
Daniel Dennett has proposed a multiple-draft view of thinking that is related to this question.(8) Given a situation of sensory experience, several unconscious conceptualizations, drafts as it were, each different in content, compete with each other, as to which is the most appropriate description for the situation at hand. The most appropriate one becomes our conscious thought. Thus, on Dennett's view different conceptual thoughts are typically concurrent and not adjoined (since they are competing). But in terms of our account, Dennett's multiple-draft view is misleading. On our account, a given sensory experience will normally deliver a single, basic, unconscious conceptualization. Such a basic conceptualization can be embellished in widely different ways in different cognitive systems, but in only one way in any given cognitive system that is driven by causal connections. Granted, multiple drafts can arise in the untypical cases where the sensory information is ambiguous with respect to the available concepts: (small furry animal), (cat?), (rabbit?). The more typical cases of multiple drafts are those that occur not at the level of conceptualization, but at the level of generating an appropriate verbal description. There we often find ourselves in a struggle, rejecting certain choices of words or word orders, because we find, before we utter them, that they do not express the conceptualization that we have.
§5. Specific and non-specific sensory perception.
We propose the following as an accurate description of three cognitive stages that occur when we perceive something. (i) During sensory perception, we have a non-specific perceptual awareness of a sensory field with spatial and dynamic features. This awareness is non-specific in the sense that, except for some parts of the experienced sensory field, the entire remainder of the field is only a general qualitative presence that lacks clarity, distinctness, and particularity. (ii) From time to time, we shift our focus of attention from one part of this sensory field to another. When we focus our attention in this way, we achieve a concentrated perceptual awareness of some specific item, characterized with specific spatial, dynamic, and sensory features. Focused attention typically occurs as a small sequence of focused attentions, as we shift our attention back and forth over a group of items of the sensory field. Episodes of focused attention thus typically have a number of different focuses that each present a specific item that is specifically featured. (iii) When we have achieved such specific perceptual awareness, we begin to think about and understand the featured items in certain ways, through the application of concepts. Our account here aims mainly at visual perception, but it describes the other types of sensory perception as well.
The three stages of non-specific perceptual awareness, focused perceptual awareness, and conceptual thought are distinct from each other. With careful introspection we can notice a slight lag between the stages as we move from the one to the other, at least in some ordinary cases, and in cases of confusion the lag is very noticeable. We grant that the cognitive system inevitably and automatically cycles through these stages, but we take this to suggest not that there is a lack of distinction but only that there are causal links. It is possible for someone to look at something, and have some sensory experience, and not perceive an individual thing with specific features, as is typically the case when our thoughts are strongly focused elsewhere. And it is possible for someone to have a focused perception of an individual thing, with specific features, and not think the usual concepts, as is typical for young infants (who have no such concepts), and even for others in cases of strong distraction, when their thoughts are led in other directions.
We suppose that sensory perception (consisting of the first two stages described above) is largely modular in Fodor's sense,(9) and that this modularity is common to our species. The sensory modules transduce the physical stimuli they receive into the generally featured representations of sensory perception, which are then available for further processing in the cognitive system. We venture no particular proposal about the mechanism that brings about our low-level perceptual awareness. We note that it must involve, at least, a never-ceasing, minimal level of processing needed for the possible detection of naturally salient features of the sensory field, which features will force our attention to them. (Such minimal processing must occur even in special cases such as sleep, for otherwise we could not be awakened by a buzzing alarm, or a poke in the side).
§6. Individuative connection.
There is an indispensable, but little acknowledged, component of conceptual thought. We are able to refer our thoughts to a particular subject. We can focus our attention on something, so that we can think of it in some way. When we see a cat in a tree, we can think (this cat) and (this tree). We are not proposing that in focused attention we have an ontological access to something in the world. Quite the contrary. In focused attention, the cognitive system isolates some part of a present complex sensory representation and represents it as a something, so that it can be processed further through conceptual representations. It is now a standard view that the phenomenal act of focusing one's attention should be construed as the increased allocation of cognitive resources towards the processing of some particular information.(10) Accordingly, we propose that when we focus our attention on some part of the sensory field, two special cognitive resources are allocated towards processing that part. (We discuss the second of these in the section that follows.)
The first resource is the activation of a special neural node that functions as a pointer to the sensory part. This node becomes temporarily connected to the sensory part, and other cognitive nodes become temporarily connected to it. The result of these connections is that the sensory part is experienced, first of all, as a specific individual item, a [this], through the temporary link with the activated pointer, and secondly, as a specifically featured item through the link with the other cognitive nodes. We will call these special nodes individuative pointers, and the temporary linkage they induce, individuative connection. It is through these pointers that the cognitive system achieves a cognitive reference to items of sensory experience. Later we will consider other ways that cognitive reference is introduced.
We are open as to how these pointer nodes are constituted, except that they cannot be taken to be the very collection of neurons whose activation brings about the sensory part of which we are aware. They must be some sort of standing nodes that become temporarily linked with the detected part, for the simple reason that these nodes continue to be active in our thoughts after the sensory representation has changed, as when the apple is not seen, as we turn our head, and we continue to think about it.
We suppose, then, that individuative connection is a fundamental operation that occurs, selectively, during the process of sensory perception. We take the number of individuative pointer nodes, [d1], [d2], [d3], etc., within the cognitive system to be large enough to accommodate moderate parallel processing. These nodes are all functionally identical as pointers, but they are numerically distinct. It is important to their function as pointers that each of them is characterized by a unique activation pattern distinct from any other activation pattern current in the cognitive system, so that our thoughts of different things are likewise distinct. And since pointers are distinguished only by what they refer to, we may call their patterns, reference activation patterns. It is also important to the function of pointers that other cognitive nodes can in turn be temporarily linked to them, to enable further processing of the items of focused attention. We speculate that when this occurs, our resulting thoughts have a superimposed activation pattern that is appropriately modified by the reference pattern of the pointer, to insure that the common referent of the different predications is preserved in our diverse thoughts. In particular, when a pointer [d] is linked with other nodes that have natural activation patterns f, g, and h, the resulting thoughts have a combined activation pattern d×f + d×g + d×h. Figures 2 and 3 illustrate the process of individuative connection.(11)
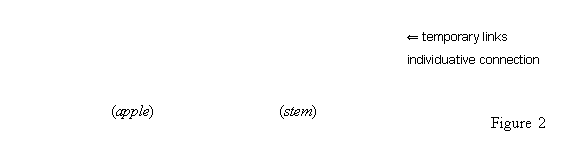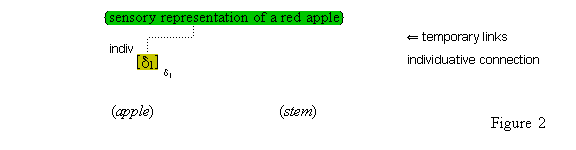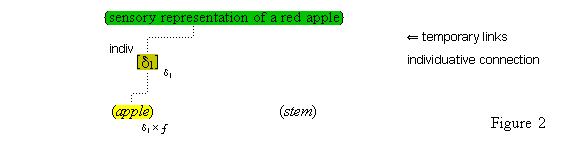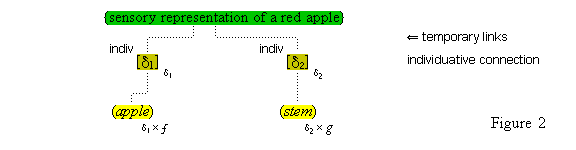
§7. Feature unit connection.
A second cognitive resource that is allocated during focused attention is a high-intensity feature detection. When we focus our attention, the features inherently present in the sensory field receive this focus as well. We become aware of sensory, kinematic, and spatial qualities in a way that we were not aware of them before we focused our attention in this way. Colors, sounds, shapes, touches, movements, are vivid, specific, and distinct. This phenomenal fact suggests that when we focus our attention, the cognitive system begins to detect features in a concentrated manner stronger than the minimal, low-level detection of features that is otherwise at work.
We propose that the process of detecting the features of our sensory experience uses certain simple prototypes of such features. We take it that the cognitive system has at its disposal a large number of cognitive nodes that we call feature units, and enough of them to accommodate the great variety of features that characterize our sensory experience. Feature units are special memory nodes that contain information for specific and simple sensory, spatial, and dynamic qualities, for edging, orientation, curvature, shape, movement, depth, color, odor, and taste. When feature units are activated, their activation brings about that enhanced perceptual awareness we have when we focus our attention.
On the empirical side, considerable research has shown that the brain engages in large-scale feature detection.(11A) A significant finding has been that the different features of an experienced object are processed in correspondingly different areas of the brain, for example, different areas for the color, the shape, and the movement of a visual object.(12) We take such findings to support the existence of feature units. An important consideration here is that feature detection, like most simple cognitive processes, occurs very rapidly, in time spans of small fractions of a second. This circumstance requires, therefore, a very simple mechanism. One can speculate about some simple procedures here. If feature units are nodes with characteristic activation patterns, and if all the sensory nodes, that are active in sensation in their characteristic way, broadcast their activation patterns in unison, then other nodes (feature units) that naturally match the broadcasted pattern will self-select, by resonating with an increased amplitude, (in the same way that sound waves of the same frequency will resonate and produce a louder sound).
We must make another important assumption about the process of feature detection, one that allows us to explain a somewhat mysterious fact: we can think different thoughts about a single thing, such as (this is apple-shaped) and (this is red), where the reference is the same. When we see an apple with a leafed stem, we detect features of the apple, and of the stem, and of the leaf. But, it is not enough to have the features {red#}, {apple-shaped#}, {green#}, and {leaf-shaped#} just be concurrently active in the cognitive system. The features {red#} and {apple-shaped#} must be connected with the apple-part, and the features {green#} and {leaf-shaped#} must be connected with the leaf-part. The simple detection of features must be accompanied by an operation that joins the detected features to a single item. So, our account requires that as an individuative pointer node is activated, the feature units that were selected during this pointing also become temporarily connected to the pointer node. We will call this two-fold operation of feature units, that is, (i) their activation in perception and (ii) their temporary link with an individuative pointer node, feature unit connection. Through this kind of connection, focused attention sensory experience results in the representation of a specific individual item that is characterized by a number of specific features. (One cannot help but notice the similarity of this account to the traditional metaphysical notion that an object of experience is a single substance in which different properties inhere.) Figure 3 illustrates individuative connection and feature unit connection when different items within a complex representation are each connected with their own feature units.
Individuative connection with its attendant featurization is not the only process that employs temporary links. Such links also occur in our speech processes. For example, the sentence "Snakes are flying telephones" produces temporary links in our thoughts of ideas never so linked, except here. Likewise, the elaborate use of pronouns in our speech evidences that concepts are also subjected to temporary links, as in, "some people admire some people because they know that others admire them." We address these issues in greater detail in section 23 below.
Admittedly, the notion of a temporary link is a somewhat difficult one, requiring its immediate creation and immediate termination, as we shift from thought to thought. But this difficulty is not peculiar to the analysis we present here. All theories must postulate some such mechanism to account for the facts of focused attention, repeated reference, and differentiated reference. Baars has made effective use of the mechanism of the global broadcasting of information throughout the global workspace of the cognitive system.(13) Information is broadcast to the workspace of the entire cognitive system, where it is then further processed by various processing units. This view implies that temporary links are at work, and it also implies the necessity of the kind of cognitive architecture we have proposed here, but which is absent from Baars' account. But the notion that information can be broadcast to processing units is an intriguing one. Combined with the notion that activations have characteristic activation patterns, the notion of broadcasting serves to explain the mechanism of a temporary link. It is plausible, then, that the constitution of our cognitive system has sufficient resources to provide the kind of temporary connections proposed here.
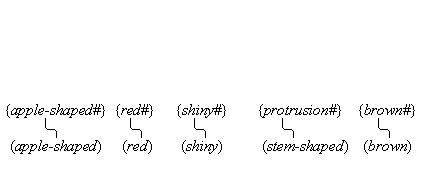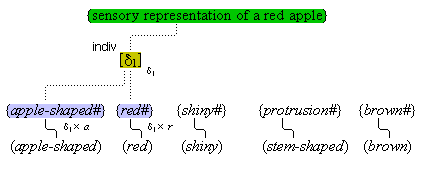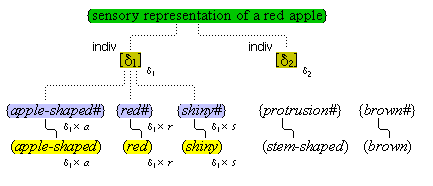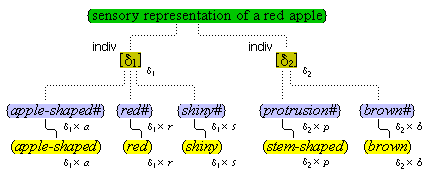

§8. Simple concept connection.
Another type of cognitive adjunction is exemplified by the case in which, when we see a shiny, red apple, we think (red), (round), (shiny). This type of adjunction is based on a permanent connection between feature units, such as {red#}, {round#}, {shiny#}, and their corresponding simple concepts, (red), (round), (shiny). We call this kind of connection simple concept connection.
We assume that many feature units (but perhaps not all), once evoked, and through re-enforced activation, come to be permanently connected with other cognitive structures. For example, the feature unit {hot#} comes to be permanently connected with certain concepts, such as (flame), and with a number of iconic memories of hot things. We take such arrangements to characterize simple concepts, such as (hot).
We first of all propose that all cognitive structures accomplish their connections through special neurons groups that we will call relay nodes. A relay node is a group of neurons that physically extends some cognitive node and becomes an interface for that node through which other cognitive nodes may connect with it. A relay node itself has no inherent representational function within the system; it functions merely to transmit the activations it receives to and from the nodes connected to it. We propose secondly that a simple concept is a relay node such that (1) it extends a feature unit and (2) it also has other cognitive structures connected to it in virtue of the conformity of these structures with the feature unit (so that, the feature unit acts as the definition for the relay node).
Thus, the feature unit {hot#} is extented by some relay node R to which are connected various cognitive structures: the concepts (flames), (the sun), (water heater), (furnace), various iconic memories of experiences we have had with hot things, as well as the word unit {"hot"}. These items have become connected to the relay node R because they all conform in appropriate ways to what acts as the definition, the feature unit {hot#}. Therefore, the relay node R is the simple concept (hot). Figure 4 illustrates the connections of the simple concept (hot).
We have then the following account of how we come to think certain simple concepts on the occasion of some sensory perception. As we focus our attention to some part of the sensory field, an individuative pointer [d] temporarily links to that part and also with a number of feature units {F#} that are activated by the given features F of the sensory part. The units {F#} in turn activate the corresponding simple concepts (F) through their permanent connections with them. (Since simple concepts are defined by their connected feature unit, we may assume that simple concepts have the same characteristic activation pattern as their feature unit.) In this way, then, a visual apple image is conceptually adjoined, when it occurs, with the simple conceptual representations (red), (round), (shiny), through the intermediate activations of a pointer and feature units. Figure 3 illustrates this process.
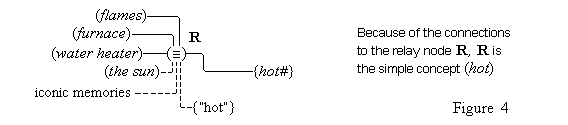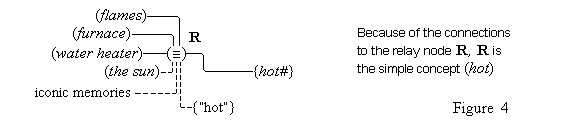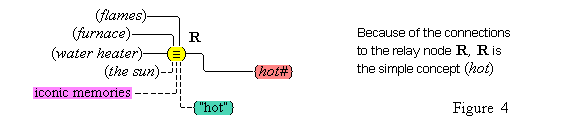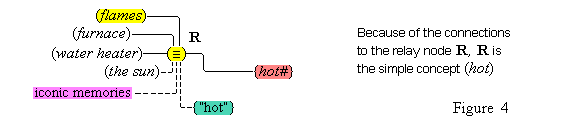
We assume an empirical origin for many, if not all, feature units. Our focus, at any rate, is on the sensory ones. The various sensory qualities that we once experienced were stored in memory to constitute corresponding feature units. Feature units, thus, contain particular sensory information, and in virtue of that, have a unique activation pattern. This account of the origin of feature units and simple concepts allows the possibility that not all human cognitive systems have the same number of feature units and simple concepts. A person's particular history of experience will determine the scope of these. But to the extent that people have similar such histories, to that extent their elementary cognitive systems will be the same. It is also worth noting that the issue of the empirical origin of feature units and simple concepts is not one that makes a difference for our account. If some feature units are not empirically derived, but are among the native components of the cognitive system, the account remains substantially the same: the occasions of our early sensory experience served to activate for the first time the native feature units, which activation in many cases continued to the formation of corresponding simple concepts.(14)
§9. Simple verbal connection.
A powerful type of cognitive adjunction is based on simple verbal connections, stored in memory, between words and concepts.(20) When we hear the word "apple," we think the concept (apple), because the two are causally connected in memory.
We note first of all that there is a distinction between the utterance of a word and the sensory perception of that utterance. An utterance "apple" varies each time the utterance is made, with variations in pitch, volume, timbre, and duration, as the individual phonemes that make up the word are produced. (Such variations may be seen on a sound spectrograph that shows the acoustic wave patterns of the utterances.) Nevertheless, we are mostly oblivious to these differences. For example, if several people were to say "apple," one after the other, we would regard them all to be saying the same word; but if they were to smack their two hands together, one after the other, producing very similar sounds, we would not regard them all to be sounding the same smack.
A plausible explanation is that, when it comes to words (as opposed to random sounds), what we hear is a stylized production resulting from a word identification process that singles out certain similarities and ignores certain differences.(21) What this means is that a stimulus, an utterance of "apple," produces in us a certain sensory representation (a heard sound) with acoustic features, features that are also produced by similar utterances. These features activate a single cognitive structure, the word unit {"apple"}, and that activation brings about a word representation, the familiar-sounding word "apple."(22) Given the considerable success of communication, we must suppose that all members of the same linguistic community have the same, or very similar, word units and representations for the word utterances of the language.
We said above that there are simple verbal connections, stored in memory, between words and concepts. In the light of the distinction we have just made, the connections exists between word units and corresponding concepts. But having made the distinction, one can often refer to word utterances, word units, and word representations as just words. Figures 4 and 5 illustrates simple verbal connection.
We consider four ways in which simple verbal connections are learned. (1) One way is through the pairing of words and items of everyday experience, a process sometimes called ostension. Our ordinary experience is such that its routine occurrence results in the formation of certain ordinary kinds of concepts, e.g. (bed), (eat), (sky), (carry), (sound), (green), (hand), (bird), and so on. (The fact that pre-verbal or deaf children engage in normal, appropriate, and intelligent behavior proves that many concepts can be, and are, formed independently of language.) When corresponding words are subsequently used by others around us, we have little difficulty in forming the appropriate linguistic correlations.
(2) A second way in which linguistic associations are made is through the process of giving a complex verbal definition for a complex concept already possessed, by means of words we understand, that is, by means of words that are already connected with concepts. This is a case in which we have an idea before we learn what word others use for it, and then we are told through words, which we understand and which single out that idea, that a certain word stands for that idea. In this way one may learn the meaning of the word "illegible," through the verbal definition "words or letters so badly written that they cannot be read," or of the word "dust-bunnies," through the description "fluffy clumps of dust that collect every now and then on bare floors," or of the word "gribble," "a tiny piece of lint, or such like, stuck to one's clothing."
(3) A third way that concepts come to be connected with words is through a process of giving a complex verbal definition for a concept not yet acquired. We are often told what a word means without us already having a concept that meets that description. Most of us at some point learned the meaning of words like "bank," "insurance," "salary," "contract," "editor," "secretary," "vice-president," "lawyer," and so on, by simultaneously learning the corresponding ideas. In this case the verbal definition is sufficient to activate all the conceptual components at hand as a combination, as indicated by the definition, which combination of concepts then becomes connected with the word. We will have more to say about such matters later under extemporaneous conceptualizations.
(4) A fourth way that a word can come to be connected with a conceptual structure is not through a verbal definition, but merely through a verbal context in which the word is used. We often hear a word whose meaning we do not know and which is difficult for us to determine. We may succeed in learning part of the idea, and we content ourselves with, what we hereafter call, a quasi-concept. A quasi-concept is a conceptual structure that is connected with a word in such a way that the structure functions as a partial definition. For example, for many of us, the word "polyester" has only a partial definition, in as much as it is connected with the conceptual structure (some kind of synthetic fiber, as used in clothing). At some point, we may come to decide that we understand fully what such a word means, at which point the connection between the word and the operative concept is completed. Or, we may remain in ignorance, and the connection remains one between a word and a quasi-concept. We discuss quasi-concepts in greater detail in section 15. In these ways, then, simple verbal connections for words are formed and become the basis for verbal adjunctions when they occur.
It is important to note that in our framework words can readily have multiple verbal connections to various concepts and quasi-concepts, and thus have different meanings, that may or may not have some commonalities. Since we can observe that our words do indeed have different meanings, we have here something that speaks in favor of our theory. As we shall see, different verbal connections can arise indirectly through a commonality in definition, as when cats and dogs are both referred to as "animals," or through some analogy, as when events are referred to as "steps," or through a paradigm shift, as when a type of chemical compound is referred to as "water." Severe puzzles about the possibility of concept change have easy solutions (cf. what Quine said, section 19), and fuzzy discussions about family resemblance meanings can be clarified (cf. section 16).
§10. Undenominated concepts.
Let us call concepts that have words connected with them denominated concepts. If one takes concepts seriously, and takes a recognition to be a criterion for the existence of a corresponding concept, then one must conclude that perhaps most of our concepts are undenominated. Simple reflection on the features of the objects around us confirms this conclusion. We have full familiarity with things that we have trouble describing with words. Easy examples come from the sensory qualities that we know so well. The aroma of freshly baked bread does not have a name, nor does the smell of freshly cut grass, nor do most smells, nor does the taste of mussels, nor do most tastes, nor does the feel of a freshly peeled twig, nor do most feels, nor does the color of slightly opaque water, and so on. Some people have names for such qualities, while most of us do not; as is common in all specialty areas. Yet, though we lack the names, we must posses many such simple concepts, since we recognize such qualities when experience presents them. The situation is the same for many complex concepts. What words do most persons have for the following common ideas?
(line where two surfaces intersect),
(tip at the bottom of the base of a light bulb),
(perfectly aligned sides formed by the pages of a book),
(irregularly aligned sides formed by the pages of an old French book),
(larger outer part of a paper clip),
(smaller inner part of a paper clip),
(sand tower made at the beach by dripping wet sand from one's hand),
(image drawn in the air by a moving glowing point),
(depressible button that returns upon release),
(depressible button that does not return upon release),
(frustrating pencil that has a completely used-up eraser),
(ink stroke produced by a quill pen),
(noise referred to as scratching a record),
(match-striking-surface of a matchbook),
(very, very thin paper, as one finds in Bibles and cigarettes),
(striped configuration, as in window blinds),
(page of a book that has become unglued and is now a mangled loose insert),
(folded piece of paper under a table leg to prevent wobbling),
(one side of a zipper),
(metal gizmo in a zipper that zips the zipper),
(bending a garden hose to stop the water flow),
(cupping one's hand to collect water for drinking).
And many more. For each of us, there is a list like this that is exceedingly long. Even though these concepts are undenominated, for most of us who have them, it is possible to achieve reference to them (that is, activate them) by using descriptive phrases that are sufficiently informative to single out specific types of experiences that we have had, as in effect we have just done in our display of them. We can call this linguistic device conceptual adjunction through recollection by description. This kind of adjunction is to be expected given the compositional nature of concepts, since one part of this composition is an access to our long-term memory of previous experiences. The words of the descriptive phrase activate their connected concepts, each of which in turn accesses (activates) memories of experiences that are stored under it. These activated memories in combination make us recall experiences described by the descriptive phase (if we had any such), and will also activate the concept in question (if it had been formed earlier by such experiences).
It is reasonable to ask here whether the complex process of conceptual adjunction through recollection by description is really different from the process of simple verbal adjunction. The only difference, it might be thought, is that the one employs a phrase, while the other employs a single word, which, if that were the difference, is indeed not significant. But consider that (1) a simple verbal adjunction is based on a permanent connection between a word and a concept, while a conceptual adjunction through recollection by description has no such basis. It is but a temporary linkage that ceases to exist as soon as the words die. Instead, (2) a conceptual adjunction through recollection by description makes essential use of our memory of previous experience, whereas simple verbal adjunction depends on no such link. And (3) descriptive phrases with different meanings can nevertheless achieve adjunction with the same concept, as we next explain.
Descriptive phrases always have a literal meaning that depends only on the words used in the phrase, one that is activated through extemporaneous conceptualization. For example, the phrase "sugar candy children receive on Christmas in Holland" has the literal meaning (sugar candy)(given to)(children)(on Christmas)(in Holland) for any English-speaking person that has the component concepts. But most descriptions have no corresponding concepts, and certainly most people have no concept that corresponds to the phrase in question, since they would not recognize such candy if they came across it. It is precisely as one says, "they have no idea of what we're talking about."
Descriptive phrases can function to recall certain experiences, through the meanings of the individual words, so as to access a concept that characterizes those experiences. In such a role, the literal meaning of a phrase may not be significant, so long as it does the job. The three phrases "sugar candy children receive on Christmas in Holland," and "sugar candy children receive on St. Nicholas day in Holland," and "sugar candy children receive on Easter in Holland," all have different literal meanings, (since three different days are involved). Yet, for all those who have enjoyed such candy, the same concept is invoked, one that for Dutch children is denominated "suiker-beestjes," translated, "little sugar-beasties."
§11. Feature units as the basic units of meaning.
Above we postulated the existence of feature units, and we discussed the role these units play in the process of perception. But these units have a larger place in the cognitive system than being a stage in the perceptual process. What is important about feature units is that they have semantic content, and, because of their foundational role, they must be considered to be the fundamental units of meaning. It is these units that ultimately give our words and thoughts the meaning that they have. Other cognitive items have a derived meaning, but feature units are inherently meaningful, and it is always this meaning, in various combinations, that is accessed by our concepts and propositions, and thus also our words and sentences, as we shall explain. Our earlier discussions make it clear that feature units are the building blocks out of which all our simple concepts are made. Simple concepts, in turn, are the building blocks out of which all our complex concepts are made. Furthermore, as we shall see in section 23, simple and complex concepts are the building blocks out of which all our propositional thoughts are built. The meaning that feature units have is thus accessed by and bestowed upon all our concepts and propositions thoughts. There is another, secondary source of what may be called meaningful content, namely, the content that our individual units of iconic memory have, in virtue of their quasi-perceptual nature. As we shall discuss in section 20, iconic memory units are linked to (and thus organized by) our concepts, and function as examples of what our concepts mean. But memory is not an original source of meaning. It is rather a record of an original perception to which meaning was attached by feature units. We propose, then, that apart from the meaning that feature units provide, there is no other source of meaning content. We propose that there are very many feature units, of varying types, and below we group them as sensorial, geometrical, kinematical, substantival, and gestalts feature units.
Many feature units have a qualitative sensory content. Such units presumably have an empirical origin, somewhat according to the following lines. The cognitive system has a basic structure of receptor nodes (that respond to external stimuli) and sensory nodes (that respond to receptor nodes) whose activity constitutes a number of different sensory fields, or sensoriums, composed of a vast number of varying kinds of sensory experiences, such as for example, redish sights, pleasing sounds, and pineapple-like tastes. When experienced, such tastes per se are stored in memory. The cognitive system has the demonstrated ability to selectively store in memory the information of an isolated qualitative feature,(14b) the pineapple taste per se, devoid of any of the other information that attended the tasting event (although there may, of course, be other, more complex, memories of those attendants as well). We identify the taste feature unit {pineapple-taste#} with the memory of the experienced quality of that very taste (or range of tastes), and once made, this feature unit is later applied to the activity of the gustatory sensorium.
Before we venture a closer look at feature units, there is a question as to how we shall refer to them in the present discussion. When a feature unit is incorporated into a simple concept that has a name, we can take the opportunity to refer to it by means of that same name. For example, the taste word "pineapple" denotes the simple taste concept (pineapple-taste). So, this is an opportunity to also use this word to refer to the corresponding feature unit. (The reader should not be alarmed that we here use names to refer to items that go, in fact, forever nameless. This is our heuristic device to make plausible our claims that these items exist and that they have a character with which we are intimately familiar.) As it happens, all the sensorial feature units seem to fall into larger ranges of varying intensities, and our concept words usually pick out subranges of those intensities. We use "#", with or without subscript, as an indicator of a certain degree of intensity. We can thus refer to the feature unit that defines the simple taste concept (pineapple-taste) by using the term "{pineapple-taste#}", or rather the term "{pineapple-taste#min} — {pineapple-taste#max}", since, strictly speaking, that concept picks out a range of taste intensities. Note, incidently, that the feature unit range {pineapple-taste#min} — {pineapple-taste#max} is just a feature unit subrange of the feature unit range {taste#min} — {taste#max}. In general, those feature units that are incorporated into simple concepts denominated by the word W, can be referred to by the term "{W#}", or by the range term "{W#min} — {W#max}". As to those many feature units that are not incorporated into simple concepts, or else incorporated into simple concepts that have no name, we clearly have no easy way to refer to them.
We group feature units into sensorial, geometrical, kinematical, substantival, and gestalt feature units. This classification and itemization has some heuristic value, but we present it provisionally. Certainly, the organization can be varied, and there are missing items, and some listed items are perhaps better considered as complex concepts. Sensorial feature units. These include the following:
- various color quality-intensities {color#}, including the various intensities {red#}, the various intensities {green#}, etc.
- various sound quality-intensities {tone#}, including the various {flute-note#}, the various {bell#}, the various {buzz#}, etc.
- various taste quality-intensities {taste#}, including the various intensities {sweet#}, {pineapple#}, {banana#}, {acrid#}, etc.
- various odor quality-intensities {odor#}, including the various intensities {pine-scent#}, {burnt#}, {rose#}, {putrid#}, etc.
- various tactual quality-intensities {touch#}, including the various intensities {smooth#}, {pressure#}, {warm#}, including {hot#}, {cold#}, etc.
- various feeling quality-intensities {feeling#}, including the various intensities {pleasant#}, {painful#}, {dizzy#}, {queasy#}, {giddy#}, {happy#}, {anxious#}, {eager#}, {want#}, etc.
- qualities of spatial orientation: {here}, {left}, {right}, {horz}, {vert}, {slant#}, {nearness#}, {location/there},
- qualities of linearity: {point}, {path}, {straight}, {open}, {closed}, {juncture}, {curve#}, {extension#}, etc.
- qualities of temporal orientation: {now}, {before}, {after}, {occur}, {duration#},
- qualities of dynamic aspects: {change}, {begin}, {cease}, {augment}, {diminish}, {movement#}, in particular {slow}, {fast}.
- qualities of being: {myself}, {other/those}, {being}, {unit}, {set}, {expanse}, {part-of}, {union},
- qualities of comparison: {same}, {opposite}, {size#}, in particular {more}, {less}, {great}, {small},
- qualities of agency: {power}, {resistance}, {goal}, {action}, {aware}, {living},
- the queral quality {wh?},
- qualities of value: {value#}, in particular {good#}, {bad#}, {just#}, {harmful#}, {valuable#}, {desired#}, {attraction#}, in particular {beautiful#}, {ugly#}.
- {horse-shaped#}, {"to be or not to be, that is . . ."}, {"a"}, {"dog"}, {barking#}, {tune of Happy Birthday#}, {mom's face#}, etc.
Some of our concepts, such as (horse-shaped), do not incorporate an individual feature unit but rather a collection of them. But these are a special kind of collection. They are an automated sequence of feature units. What is characteristic of automated sequences is that when a part of the sequence is activated, the entire sequence is activated. This is most likely the manner in which we hear words and sentences, as is evidenced by the fact that we can hear one word even though another word is spoken to us. And it is likely that a great deal of sensory perception involves such automation, in the sense that prior sensory experience generates in memory certain automated sequences of feature units which are thereafter made use of by the cognitive system in its processing of sensory information. We note that, in the same manner that feature units are pre-conceptual, automated sequences of feature units are pre-conceptual. Also, we will suppose that what is widely known as gestalt perception is to be understood in terms of automated sequences of feature units. On this view of gestalts, one can account for their holistic character.
We make some further observations. First, the explanatory framework that we have been presenting seems to require certain answers to the question of the origin of our concepts.
The events of our ordinary experience provide the cognitive system with the occasions that lead to the creation of feature units, as we just described above. And these events also provide the circumstances that lead to the further formation of corresponding simple concepts. Moreover, it is generally true that without those opportunities and circumstances, we will not possess the feature units and simple concepts in question. In fact, all of us have lacked certain basic, sensory experiences, and all of us, therefore, do not have the corresponding feature units, nor the corresponding simple concepts. For example, children who have not been subjected to this color and to that taste, will lack the color feature unit, say, {color#23} and the taste feature unit {pineapple-taste#}, as well as the corresponding simple color concept (lavender) and the simple taste concept (pineapple-taste). In this sense then, (many of) our feature units and simple concepts have an empirical origin: They were brought about by certain kinds of experiences, and without those kinds of experiences, they would not have been so formed.
Below in section 15, we discuss a different circumstance. Since we all live in a language community, we all acquire special conceptual structures, that we may call quasi-concepts, that mimick to a certain extent concepts that we do not have (but which other people do). For example, someone who has never seen anything like lavender, could nevertheless form the complex conceptual structure (some kind of)(pale)(bluish)(redish)(color) and have the word "lavender" associated with it. But that conceptual structure has a meaning altogether different from the simple concept (lavender) that is defined by the simple feature unit {color#23} that was once experienced.(22a)
But there is an equally important sense in which our feature units and simple concepts do not have an empirical origin. It is true that the events of experience produce these items — but only as items constructed out of the materials of the cognitive system, and only as items constructed in accordance with the forms that the cognitive system is capable of producing. There are easy examples of this. We are not capable of having the sensory experience that many other species have: we cannot have the auditory sensations that dogs have; we cannot have the olfactory sensations that many animals have; we cannot see in the visual spectrum that many insects and animals can. Consequently, we cannot form such auditory, olfactory, and visual feature units and simple ideas. Moreover, all of the sensory experiences that we do have are characterized by sensory qualities that cannot be characteristics of physical objects, by all scientific accounts. Such qualities, therefore, must have been concocted by the cognitive system. We feel warmth, but only energy characterizes physical objects. We hear sound, but only air particles are vibrating. We see color, but only light-waves are being reflected. We feel dizzy, but no physical thing has a physical property like that. We conclude, then, that there is a double factor production of our feature units and simple concepts. One factor is empirical: the events of our experience causally produce these items. The other factor is innate: the cognitive system manufactures these items out of its own materials and according to its own design.(22b)
Such manufacture is not limited to sensory items. We experience a spatial expanse around us, that is characterized by the slopes of perspective, by parts that are far and near, and by a Moon that is sometimes the size of a dime and sometimes the size of a quarter. We experience a flow of time with a present, past, and future. We experience a here and now with change and becoming. These characteristics do not characterize the physical world itself. The space and time that we experience is something we experience: it is a mental fabrication. (We are not ready at this point to argue that all feature units involve a double factor production. It is possible that some of the feature units we have labeled as substantival are entirely innate.)
A second observaton deals with a puzzle about whether simple concepts have feature units as their definition. In the framework we have presented, concepts such as (cold) and (blue), and most other sensory concepts, appear to have two incompatible kinds of meaning: they have a simple definition and a complex definition as well. On the one hand, the concept (cold) has as its meaning the sensation that we know so well, the feature unit {temp#}, which is a simple definition. But on the other hand, the concept (cold) has the complex definition (low) (temperature). Similarly, it appears, on the one hand, that (azure) has the simple definition of the visual quality that we experience when we look up on a cloudless day, namely the feature unit {azure#}, and, on the other hand, that (azure) has the complex definition (sky-blue)(color). Actually, the solution is quite straightforward. We must take care to distinguish between the simple concepts and the complex concepts that go under the same names. When we use a word such as "blue", there is a slight, but harmless ambiguity as to whether we mean the sensory quality or the color category. There is the simple concept (blue), which has as its definition the feature unit range {color#a} — {color#c}. There is also the complex concept (blue*), which has the definition (blue)(color). The same thing can be said for many other sensorial concepts. The simple concept (cold) is a sensory quality and has as its definition the feature unit range {temp#min} — {temp#b}, while the complex concept (cold*) denotes a temperature category and has the definition (cold)(temperature). One qualification to these points. The cognitive system may never have gotten around to generating the complex version of the concept in question, which is a likely outcome, given the redundancy involved, in which case the ambiguity we mention would not exist. Figure 4A illustrates these points in some detail.
To all this we add a closing observation. It is interesting that there are in many cases several cognitive items that are very closely related in meaning and function, for example: (1) a redish section of the visual field of a visual experience; (2) the feature unit {red#}; (3) the simple color concept (red); (4) the complex color concept (red)(color); and (5) the word "red". And then, there is (6) the non-cognitive item to which all these cognitive items apply: that prominent characteristic of the rose before us.
| concept | type | simple definition / feature unit | complex definition |
| (azure) | simple | {color#a} — {color#b} range | ××× |
| (azure*) | complex | ××× | (azure)(color) |
| (blue) | simple | {color#a} — {color#c} a < b < c | ××× |
| (blue*) | complex | ××× | (blue)(color) |
| (color) | simple | {color#min} — {color#max} | ××× |
| (color*) | complex | ××× | (color)(feature) |
| (cold) | simple | {temp#min} — {temp#j} | ××× |
| (cold*) | complex | ××× | (low)(temperature) |
| (frigid) | simple | {temp#min} — {temp#k} k < j | ××× |
| (frigid*) | complex | ××× | (extra low)(temperature) |
| (temperature) | simple | {temp#min} — {temp#max} | ××× |
| (temperature*) | complex | ××× | (temperature)(feature) |
| Figure 4A | |||
§12. Simple and complex concepts.
Our account supposes that there is a difference between simple and complex conceptual representations, and a corresponding difference between simple and complex concepts, whose activations bring those representations about. We will not present a formal account of complex concepts until section 13, but it is useful to make some preliminary remarks about the distinction at this point.
Simple concepts are the low-level conceptual distinctions that the cognitive system is able to make, and complex concepts are special combinations of simple ones. For example, the concept (red) is simple, and it is defined by a feature unit of a range of certain sensory color intensities.(15) The concept (apple) is complex, and it is defined by the component concepts (apple-shaped), (apple-flavored), (apple-textured), (apple-skinned), (edible), (fruit).(16)
But what are combinations? It makes a difference how one answers this question, as an early argument by Fodor shows: All human beings have the same simple concepts. (Let's agree that something close to that is the case.) So, all human beings have all the same negations of those concepts, and all the same conjunctions, and all the same combinations of all those concepts under whatever operations human beings have for combining concepts. So, if complex concepts are combinations of simple ones, then all human beings have the same set of complex concepts. Indeed, Fodor concludes that all human beings have all the concepts that are possible for human beings.(17) But on our account, at least, some people do not have the concept (telephone).
The argument supposes that whenever someone has some concepts, that person also has the combinations of those concepts through the application of various operations, so that when someone has the concepts (eats), (apple), and (yellow), he also has as concepts all the combinations of those concepts, such as, (does not eat), (yellow non-apple), (eats only non-yellow non-apples), and so on. But why should we accept the unsupported claim that we have such concepts as well as many others even more foreign to our thoughts? It is true that we are able to entertain such thoughts, on certain occasions, as when we hear such phrases, but that does not show that we have such concepts. Later, in section 22, we will show how we normally have such thoughts without having such concepts. Let us say here that we take concepts to be permanent structures of the mind, once we have them. Such structures are formed through the formation of permanent connections among their components, and such connections are formed only as a consequence of the experiences we have, including our inner cogitations. So, if our experiences fail to form certain connections among our concepts, then certain complex concepts will fail to be formed. Putting the matter more formally, we can say that the domain of concepts is not combinatorially closed under its operators; and in this regard, our account gives significantly different results from accounts that postulate such closure.
The distinction between simple and complex concepts has an important result. Early empiricists, like Hume and Berkeley (but not Locke), based their epistemology and philosophy of mind on the view that all concepts are particular sensory images, memories of the experiences we have had, with names attached to them.(18) But one consequence of making the distinction between simple and complex concepts is the conclusion that there are no sensory images that define complex concepts, such as (apple), (sunset), (song), (elephant), and so on. This consequence seems, at first sight, to be counter-intuitive, since such concepts are paradigms of "ideas derived from experience."
Nevertheless, both philosophical reflection and empirical results force us to conclude that complex concepts cannot be defined by any complex sensory images stored in memory. (1) A concept such as (apple) is far too general in its conceptual scope to be defined by some specific, complex sensory image, or even set of images. The apples of experience are of many different types and are situated in many different circumstances, and the concept (apple) applies to them all, as well as to an indefinitely large number of possible variations. But, no sensory image of an apple, being particular, applies to more than one apple. Complex sensory images, then, are far too particular to be able to define a general complex concept. (2) On the other hand, every complex sensory image lacks a focus of application. An image of Grandma holding an apple is also one of Grandma, of her clothing, of her posture, of the wallpaper, of her nose, of her hand, of holding, of an apple, of an apple-skin, of an apple-shape, of an apple-color, and so on. How can an image of many diverse things be construed as a definition of the concept (apple)? An appeal to a set of such images will not help, because (3) if a complex concept were to be defined by a set of complex sensory images, what would be the criterion in virtue of which such an image were a member of the set? Presumably, some sort of similarity principle. But that would require a method of sorting images in terms of common simple features, together with a composition principle, both of which are rejected by the theory in question. (4) Finally, experimental results argue against a definition by complex sensory images. Extensive research in feature detection has shown that sensory perception occurs through the parsing of the sensory field into distinct features. Experiments show that visual perception begins with the detection of low-level features, such as the determination of color edges, and continues with the separate processing of separate features, such as color, shape, and movement, in different parts of memory.(19) The visual system is therefore causally incapable of isolating a complex visual sensory item without also parsing its component parts. The compositional character of feature detection in sensory perception strongly supports a compositional hypothesis in concept formation and application. These standard arguments force the conclusion that it is not the case that complex concepts are defined by complex sensory images stored in memory, so that it be in virtue of such images that we think a complex concept when we perceive a complex impression.
But all of this is not to deny that we have, in many cases, complex sensory images stored in memory and connected with complex concepts. Indeed, there is nothing more familiar than our pictorial memories, as we discuss below under iconic memory connections. But they play a secondary role, and our account proposes that they can be elicited only through the prior activation of concepts: first we think the concept, say, (elephant), (zoo), or (circus), and then we think our elephant memories.
§13. Analytic connection.
When one considers the constitution of concepts, one must unavoidably conclude that many concepts are combinations of other concepts, and that there are connections among concepts that are inherent in the very organizational structure that they have. Concepts are thus seen as having definitions, and the connections between a concept and its parts are seen as analytic relations.
Within a framework of neural nodes, there is no mystery about what definitions and analytic relations are. Let us consider the following situation. Two conceptual nodes (edible) and (nourishing) are permanently connected to a conjunctive operator node [∩] in such a way that they are its operands. The node [∩] thus forms the conceptual structure (edible and nourishing). Operator nodes are always extended by some relay node R whose function it is to enable connections to other nodes and transmit activations. (Relay nodes have only this formal function.) Since the structure at hand is conjunctive, the simultaneous activation of the two nodes (edible) and (nourishing) is both a causally necessary and a sufficient condition for the activation of the relay node R, and in this regard one may consider the conjunctive structure to be the definition of R, but we say more on this point shortly. The relay node R is in this way a complex concept and has the definition (edible and nourishing). R thus turns out to be the concept (food). Figure 5 illustrates the connections at issue.
Our account proposes that there are conceptual operator nodes that combine individual concepts into permanently connected structures of concepts, which are our complex concepts. We distinguish three kinds of conceptual operator nodes: conjunctive, negative, and potentive operator nodes, that we can render as,
 0,
0,  1,
1,  2, . . . , [non]0, [non]1, [non]2, . . . , [can]0, [can]1, [can]2, . . . , respectively. These operators form many of our complex concepts, for example,
2, . . . , [non]0, [non]1, [non]2, . . . , [can]0, [can]1, [can]2, . . . , respectively. These operators form many of our complex concepts, for example,
| (food) : |  — — —(edible)—(nourishing) —(edible)—(nourishing) |
| (poison) : |  — — —(substance)—(produces)(ill-health) —(substance)—(produces)(ill-health) |
| (bachelor) : | 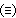 — — —(adult)—(male)—[non]–(married) —(adult)—(male)—[non]–(married) |
| (blind) : |  — — —(has eyes)—[non]–[can]–(see) —(has eyes)—[non]–[can]–(see) |
| (invisible) : |  —[non]–[can]–(be seen) —[non]–[can]–(be seen) |
| (unbendable) : |  —[non]–[can]–(be bent) —[non]–[can]–(be bent) |
| (even number) : |  — — —(number)—(multiple of )(2) —(number)—(multiple of )(2) |
| (elephant) : |  — — —(elephant-shaped)—(animal) —(elephant-shaped)—(animal) |
| (telephone) : |  — — —(contraption)—(is for)(long-distance talking) —(contraption)—(is for)(long-distance talking) |
| (nourishing) : |  —(produces)(health) —(produces)(health) |
| (violinist) : |  —(plays)(violin) —(plays)(violin) |
| (conductor) : | 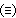 —(conducts)(orchestra) —(conducts)(orchestra) |
| (drives) : | 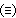 —(controls)((movements)(of)(some vehicle)) —(controls)((movements)(of)(some vehicle)) |
In addition to conceptual operator nodes, there is another operation that leads to complex concepts, namely, relational complementation, where a concept is connected to one of the arguments of a relational concept to form a complex concept. Since we discuss relational concepts in section 17 below, we here only mention some examples, namely, the last four listed above.
We emphasize two points here. (1) The first one concerns the true nature of concepts. All concepts, (tree), (yellow), (love), (number), (telephone), all of them, are merely relay nodes, and as such, they, by themselves, have no inherent representational function in the cognitive system. They are nodes that exist only to form permanent connections to other cognitive nodes and transmit activations through them.(23) This may seem highly counter-intuitive, until one considers that the other kinds of cognitive structures (namely, sensoriums, feature units, iconic memory) do have a content, which they indirectly bestow on all the relay nodes that directly or indirectly connect to them. (2) The second point is that concepts perform their essential relay function under a condition. Concepts have and acquire connections to other nodes only when those nodes conform in an appropriate way to the definitions of the concepts. Connected concepts and iconic memories have this conformity, as we shall show; and names become connected to concepts because those defining structures turned out to be the cognitive structures that were operative when the words were being learned. (3) We mention also a third point, namely, that we continue our earlier speculations regarding activation patterns. Since a complex concept has a definition, we will suppose that the activation pattern of a complex concept is simply the superposition, say, a + b + c + . . . + s, of the activation patterns a, b, c, . . . , s, of its component parts.
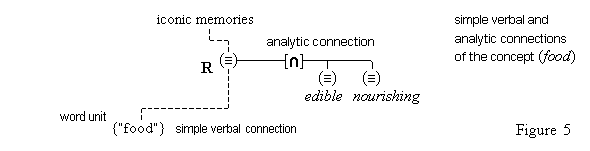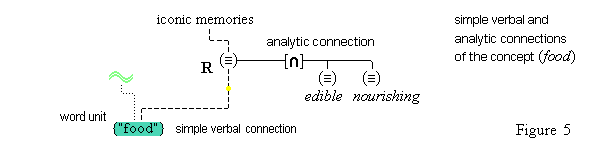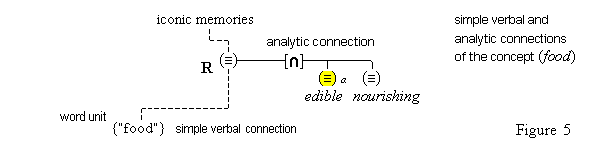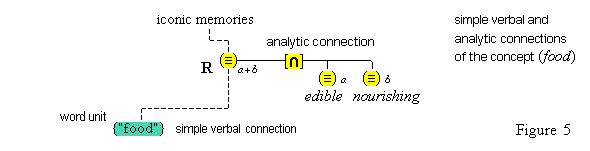
§14. The non-existence of disjunctive concepts.
We proposed above that there are three types of conceptual operator nodes, namely, conjunctive, negative, and potentive operator nodes, that function to combine individual concepts into the permanently connected structures that are our complex concepts. We rendered these operators as
Conspicuously absent from this list are the customarily recognized, so-called disjunctive operators: [or]0, [or]1, [or]2, . . . . This absence is not because of some difficulty with regard to a formal grammar of disjunctive operators, since the latter would just mirror the formal grammar of conjunctive operators. The difficulty is rather more substantial and arises on several fronts.
(1) There is a problem about what disjuntive conceptual structures would be in their concrete construction. For example, a conjunctive operator applied to the concepts (food) and (expensive) produces the concept [∩](expensive)(food), which is the concept (expensive food). That this construction is real, that is, that it is a working concept for most of us follows from the fact that most of us have a list of intelligible things to say specifically on the topic of expensive food, a list that cannot be compiled by consulting the two such separate lists on the topic of expensive things and the topic of food. Along the same lines, we also have a list of instances in memory under the topic of expensive food. So, we have thoughts and memories about expensive things, and we have thoughts and memories about food, and we also have additional thoughts and memories about expensive food.
But how would the story go for a structure like (food)[or](expensive)? The hierarchical and hub-like function that is characteristic of concepts has no place here. What instances in memory would be connected to it? Perhaps, some memories of some bananas, a Rolls Royce, some mashed potatoes with gravy, a new office building? But for what conceivable purpose would such a diverse list of items be available? Again, what strong connections of such a structure would there be to other ideas, brought about by constant experience? There would be none, since there are no rules of experience that hold for things that are food or expensive. On the basis of these considerations we conclude that we have no evidence whatsoever for thinking that structures like (food)[or](expensive) exist, since they lack key characteristics of concepts, and for that same reason, we have evidence for thinking that such structures do not exist.
(2) On the theoretical side, there is a more serious problem regarding the very thinkability of disjunctive concepts. We have proposed that all concepts have activation wave patterns, whose activity constitutes their being thought. Moreover, nature provides the circumstance of the superposition of two or more wave patterns, as we have already discussed. For example, the activation wave pattern for [∩](food)(expensive) is the complex wave pattern f + e. But superposition is the only circumstance that nature provides for the construction of complex waves: in particular, there are no complex wave patterns that display two waves as alternatives to each other. That means, then, that disjunctive conceptual structures cannot be thought, since there is no activation wave pattern that thinks them. Below we consider a different kind of cognitive structure that is disjunctive.
(3) There is also the problem of vacuity. On closer examination, there are no examples of disjunctively defined concepts. Now this may seem to be very counter-intuitive, and one might propose a large number of very ordinary concepts as candidates of disjunctive concepts, such as, (parent), (sibling), (spouse), (congressman), (college class), (eating utensil), or (bicycle part), with definitions such as:
|
(parent of x)
(sibling of x) (spouse of x) (congressman) (eating utensil) (college year) |
= (mother of x) [or] (father of x)
= (brother of x) [or] (sister of x) = (husband of x) [or] (wife of x) = (senator) [or] (representative). = (knife)[or] (fork) [or] (spoon) [or] (chopsticks) = (freshman yr.) [or] (sophomore yr.) [or] (junior yr.) [or] (senior yr.) |
(It is easy to arive at these analyses. Just think of a category, and then list all the different types of things under that category. If you have an exhaustive list, then you are done.) In favor of these analyses one can note that the disjunctive components turn out to be the subcategories that correctly exhaust the given category. So, it must be admitted that these analyses do provide factually correct conditions for the application of the concepts, just as definitions do. Do you now see an eating utensil before you? Then you now see a knife, a fork, a spoon, or chopsticks. Do you now see a knife, a fork, a spoon, or chopsticks before you? Then you now see an eating utensil. This much is correct. Nevertheless, these analyses cannot be the definitions of the concepts at issue. First of all, these analyses are too restrictive. They correctly describe the way things actually are, but one can surely imagine other possibilities. Surely, the ordinary idea of eating utensil allows that there can be, even if there are not any, other kinds of eating utensils besides knives, forks, spoons, and chopsticks. And so too for the other proposals. This much alone forces us to reject the above listed proposals as definitions.
Secondly, one must consider how the disjunctive components themselves are defined. A little reflection shows that all the listed disjunctive components must themselves be defined in terms of the very concepts they are meant to define. This circularity becomes apparent when one considers their rather obvious definitions:
|
(mother of x) (brother of x) (husband of x) (senator) (knife) (freshman yr.) |
= (female) (person who raises x) = (male) (has same parent as x) = (male) (is married to x) = (member of Congress) (in the Senate) = (sharp-bladed) (tool used for eating) = (first) (year of college study) |
– this defn. contains (parent of x) – this defn. contains (sibling of x) – this defn. contains (spouse of x) – this defn. contains (congressman) – this defn. contains (eating utensil) – this defn. contains (college year) |
We conclude that none of the proposed disjunctive analyses listed above qualify as definitions. Which brings us back to the problem of vacuity: There are no examples of disjunctively defined concepts.
While we reject the existence of disjunctive concepts, we grant the existence of disjunctive structures of a different type, namely, disjunctive propositions. Certainly, we have the word "or" that functions as a grammatical operator on sentences. We can say sentences like
"it is expensive, or it is fashionable."A basic assumption that we make in this article is that sentences derive their meaning through the association that words have with corresponding cognitive items. So, we grant the existence of disjunctive cognitive structures such as the following:
(it) [is] (expensive) [OR] (it) [is] (fashionable).We must wait until Part III on Propositions and section 28, to explain how the elements of this structure are formed. Suffice it say here that this structure has been formed in an extemporaneous manner through the use of a propositional operator node [OR] that operates, not on concepts, but on propositions that are extemporaneously and momentarily formed. What is important here is that, while concepts are permanent structures once they are formed, all propositional structures have but a momentary existence that lasts about as long as the duration of the utterance of the sentences that express them. This means, in particular, that we are able to temporarily think disjunctive propositional thoughts. On the other hand, such thoughts, being momentary, are not in any sense disjunctive concepts.
§15. Quasi-concepts.
There is a related situation that our linguistic repertoire contains words that we do not fully understand, that is, words for which we have no complete, corresponding concept. The normal circumstances of our lives permit us to be ignorant about a great many things that some other people know about. Because of this, our language employs many notions which we understand only partially, although enough to get by on. These words are permanently connected with certain conceptual structures, and are, what we call, the quasi-concepts of those people who find themselves in this predicament. Consider the following list of words: beech, polyester, rayon, calcium, vitamin A, fluoride, pH-balance, X-ray, microwave, radar, electricity, voltage, octane, gene, DNA, sonata, concerto, Calvinist, Mormon, tango, jitterbug, gigabyte, megahertz, and many more. For most of us, the list is embarrassingly long.
Words for quasi-concept are not just words for which we are not able to supply a definition on demand, since that happens also with words that we understand fully, for example, "slush," "howl," "paper," "water," "house." Quasi-concept words are words that we do not understand fully because they are the verbal associates of conceptual structures that are explicitly conceptually incomplete. Octane, we say, is some kind of a combustion quality of gasoline; a microwave is some kind of radiation; an X-ray is some kind of radiation; vitamin A is some kind of a nutrient necessary for health; polyester is some kind of a synthetic fiber, a Calvinist is some kind of religious Protestant; and so on.
It would not be unreasonable to suppose that our cognitive systems have at their disposal a number of simple conceptual incompleteness nodes:
(some kind of )1, (some kind of )2, (some kind of )3, ...,all distinct, yet all functionally identical. (Perhaps, relay nodes with no other attachments could play this role here.) These incompleteness nodes would combine with concepts to form quasi-concepts. The word "octane" would then be verbally connected with the conjunctive structure
Our conceptual repertoire thus contains (1) denominated concepts, (2) undenominated concepts, and (3) denominated quasi-concepts.(24) Later, we also introduce (4) extemporaneous conceptualizations.
§16. Family resemblance accounts of concept meaning.
Many words in our language have a number of different meanings, in at least two different ways. First of all, words can be ambiguous with respect to the general type of thing at issue. The word "chair," for example, can denote a piece of furniture, or an action of presiding over something, or a person who performs such an action, or a distinguished professorship. Such a general level of ambiguity is normally not a problem, since the context in which words are used usually reveals which meaning is at issue. This applies also to circumstances such as metaphor and simile, in which we intentionally misuse words to attribute ideas that are not literally applicable: A drawing of a chair, a paper maché construction of a chair, a doll chair, or some other resemblance of a chair, may all be called a "chair," in a derivative sense.
There is also a second kind of ambiguity that words have, even when they are understood within a specific general sense, such as, "chair" as a piece of furniture. We use the word "chair" to refer to a common chair, an armchair, a desk chair, a swivel chair, a rocking chair, and so on. Again, this is generally not a problem since all these kinds of chairs are chairs. But a question arises about the meaning of the word "chair," and other words as well. Do words, when understood within a specific general category, have a single meaning, or do they have multiple meanings? Does "chair" mean one thing, or does it mean any from a number of things?
The traditional view on this matter is first, that words are associated with concepts, and in this way derive their meaning, and second, that all concepts have an exact definition, in the sense that the components of the definition are sufficient conditions together and necessary conditions individually for the correct application of the concept. (This is the viewpoint of this article.) But for some time there has been a widely accepted view that rejects the traditional view.(24a) Instead of an exact definition, a concept has a "fuzzy" definition, consisting of a number of different components, not all of which are necessary constituents. Because not all the components are necessary for the application of a concept, the fuzzy definition is actually a collection of various subgroups of the listed components. In this way, a concept forms an entire "family" of criteria, each of which has a certain "family resemblance" to the others, sharing some components but not others.(24b)
Consider, for example, the following analysis of the concept (chair): "A chair is something one sits on, that has arms, a back, and four legs." Of course, this cannot be a correct definition, since there are too many counter-examples. Some chairs have four legs, some have three, some have a central pedestal, and some are supported by side panels. Also, some chairs have arms, and some do not, and some have a back, and some do not. In the light of these points one might consider the definition, "A chair is something one sits on." But that will not do either, since one can sit on practically anything. And so, we seem not to be able to provide the definition of (chair). Similar kinds of nit-picking have similar results for other concepts, (house), (apple), (book), and so on, and so the story goes.
The conclusion that many draw from such would-be refutations is that concepts have no exact definition. Moreover, the supporting details just cited point to an alternative account, namely, that concepts have a "fuzzy definition" involving a number of different components, not all of which are necessary conditions for the correct application of the concept. The various partial combinations of these components form a family of criteria. For example, the following combinations illustrate a family of criteria for the concept (chair):
| (a) | (seat), | (has a back), | (has arms), | (has legs support), | (all rigid) |
| (b) | (seat), | (has a back), | (has no arms), | (has legs support), | (all rigid) |
| (c) | (seat), | (has a back), | (has no arms), | (has pedestal support), | (has a swivel seat) |
| (d) | (seat), | (has a back), | (has arms), | (has pedestal support), | (has a swivel seat) |
| (e) | (seat), | (has no back), | (has no arms), | (has legs support), | (all rigid) |
| (f ) | (seat), | (has no back), | (has no arms), | (has pedestal support), | (all rigid) |
| (g) | (seat), | (has no back), | (has no arms), | (has pedestal support), | (has a swivel seat) |
| (h) | (seat), | (has a back), | (has arms), | (has side panels support), | (all rigid) |
| (i ) | (seat), | (has no back), | (has arms), | (has side panel support), | (all rigid) |
| (j ) | (seat), | (has a back), | (has arms), | (has rockers support), | (all rigid) |
The uncontested existence of these employed combinations is supposed to show, first, that the concept (chair) has no definition in the traditional sense, second, that the concept (chair) is instead a family of criteria by which we apply the concept, and third, that these points are also true for other concepts. In response, we do, of course, agree that concepts have such families of criteria, and that these criteria do have family resemblances. And we agree that the criteria that make up these families are functioning items in our thinking. Nevertheless, this analysis fails to show that concepts have no definition in the traditional sense. And for a simple reason. Families and family resemblances exist even in cases where concepts do have a definition in the traditional sense. Consequently, the fact that families and family resemblances exist is no reason at all for thinking that there are no definitions in the traditional sense. Consider the combinations of components in the family of types of triangles:
| (a) | (figure), | (3 sides), | = (triangle) | ||
| (b) | (figure), | (3 sides), | (3 sides equal) | = (equilateral triangle) | |
| (c) | (figure), | (3 sides), | (60° ang.), (60° ang.), (60° ang.) | = (equiangular triangle | |
| (d) | (figure), | (3 sides), | (2 sides equal) | = (isosceles triangle) | |
| (e) | (figure), | (3 sides), | (2 sides equal), | (90° ang.), (45° ang.), (45° ang.) | = (isosceles right triangle) |
| (f ) | (figure), | (3 sides), | (no angle 90°) | = (oblique triangle) | |
| (g) | (figure), | (3 sides), | (1 angle > 90°) | = (obtuse triangle) | |
| (h) | (figure), | (3 sides), | (3 angles < 90°) | = (acute triangle) | |
| (i ) | (figure), | (3 sides), | (90° angle) | = (right triangle) | |
| (j ) | (figure), | (3 sides), | (3 sides uneq.), | = (scalene triangle) | |
| (k) | (figure), | (3 sides), | (3 sides uneq.), | (90° angle) | = (scalene right triangle) |
| (l ) | (figure), | (3 sides), | (3 sides uneq.), | (30° ang.), (60° ang.), (90° ang.) | = (30°-60°-90° triangle) |
This group of combinations of components is the sort of thing proposed by the resemblance view. This group is a family, and its members have a family resemblance. But, it is pretty clear that this family of alternative criteria is nothing more than a group of further qualifications of the concept (triangle), and that each of these qualifications is itself a concept that has an exact definition, as for example, (scalene triangle) = (figure) (having three sides) (having all sides unequal). But more importantly, the concept (triangle), on which all these qualifications depend, itself has an exact definition, (figure) (having three sides). In all of this, there is absolutely no fuzziness of any kind.
So, it must be granted that some family concepts, such as (triangle), have an exact definition. What significance, then, does this have for other family concepts, such as (chair)? We note that it is usually just claimed that concepts, such as (chair), have no exact definition, a claim usually illustrated (as we have done above) with some popular, but naive descriptions. And it has to be noted that those who make the claim are not really trying to find any definitions, since they happen to favor an opposing theory. But when one is serious about finding definitions, they are indeed there to be found, though it may take some effort to discover them. We make one qualification. We grant that some of our ideas really are fuzzy ideas. Good examples are those ideas that we have called quasi-concepts in section 15 above. Quasi-concepts are our ideas of what other people may mean by certain words whose meaning we do not fully know. For example, we may not know exactly what the words "octane," "polyester," and "tango" mean, and, significantly, when this is so, we are actually aware of the fact that we do not have that knowledge. We know it when our ideas are fuzzy. In any event, the idea (chair) is not fuzzy.
Let's give some definitions. Our idea of a chair is centrally an idea of a certain kind of seat. So we begin with that idea. Actually, we have a several ideas of seat, each with component ideas. We note first of all that is is not enough to say that a seat is something one can sit on, since one can sit on practically anything, for example, on one's hands. Rather, a seat is something someone can sit-down-on. That is a more demanding idea. One can be sitting, and be on a mountain, or on the Moon, but no one is tall enough to sit-down-on a mountain, or the Moon. So, mountains and the Moon cannot be seats. Second, our idea of a seat is the idea of something that is raised from the ground where one is standing, typically by some kind of supports. One can sit down on the ground, but the ground is not raised from the ground, so the ground is not a seat. But a big rock, or a small prominent mound, is a seat, if one can sit down on it. Again, one can sit down on a small rug, but not being raised, it is not a seat. (Aladdin's flying carpet, on the other hand, when elevated, is a seat.)
(seat0) = (surface)(raised from the ground)(someone can sit-down-on it)
We also have several more specific ideas of seat, seats that accommodate the human body in specific ways. One can sit down on certain seats with ease, in as much as they have a certain height, that we can here refer to as a knee-high height. Included here is the idea that a seat thus raised is raised by some supports. Also, one can sit back into certain seats, in the sense of a depth covered by one's thighs, that we can here refer to as a thigh-length depth. (It is not an accident that things that are seats in these senses are things that rest our legs when they are tired.) Because these kinds of seats do not occur naturally, we have ideas of such seats that include the component idea of something that has been made. Our various ideas of chairs, stools, benches, and sofas clearly have these four components.
(seat1) = (surface)(raised from the ground)(someone can sit-down-on it)
(was made)(has supports)(knee-high height)(thigh-length depth)
Even more specific ideas are seats that are not long, but somewhat narrow, to accommodate one person, with a width that we may call a single width. Clearly, our various ideas of chairs and stools have that component. On the other hand, there are ideas of seats that are long, quite a number in fact, including ideas of various kinds of benches and sofas.
(seat2) = (surface)(raised from the ground)(someone can sit-down-on it)
(was made)(has supports)(knee-high height)(thigh-length depth)
(single width)
(seat3) = (surface)(raised from the ground)(someone can sit-down-on it)
(was made)(has supports)(knee-high height)(thigh-length depth)
(long width)
Our various ideas of chairs are more specific still, and have the component idea of having rests, which are pieces added to seats for the comfortable resting of the body: the arms (arm rests), the back (a back rest), the head (a head rest), the shoulders (wings), but not the legs, as they are rested by the seat. The presence of any rests make it appropriate to say that one sits in a chair.
(chair0) = (surface)(raised from the ground)(someone can sit-down-on it)
(was made)(has supports)(knee-high height)(thigh-length depth)
(single width)
(has rests)
Figure 5b
We can continue with greater detail. Such a seat without rests is not a chair but a stool. A seat with a back but no arm rests is a common chair. An X-shaped roman chair is a seat with arm rests but no back. A seat with back and arm rests is an armchair, and so on. Additional distinctions arise when one considers the different types of supports that seats can have that raise the seat from the ground. Common ideas of supports are legs, pedestals, side panels, and rockers, each of which defines a corresponding type of chair. Also, the ideas of being upholstered, or not, are further distinctions for all sorts of seats. Figure 5b shows how all these various ideas are defined and related.
We have seen, then, that we have a number of seat concepts, ranging from the very general to the more specific. Among the latter is a general concept of chair as well as more specific chair concepts. We have also seen that these seat concepts and chair concepts form large, related families whose members have a family resemblance. What is important here is that all these concepts have exact definitions and that these concepts are hierarchically arranged. One general combination of component ideas defines a family, and all other combinations of component ideas that belong to that family do so because they are further qualifications of some other member of that family.
Of course, our intention here has not been to just talk about seat concepts and chair concepts. We have used these examples to argue against an important but nevertheless erroneous view of the nature of concepts, and along the way, we have illustrated the traditional view of the matter.
§17. Relational concepts.
Our thoughts are not always simple predications, that is, are not always attributions of some property to some item of reference. When we see a cat sitting in a tree, we can think not only (this cat) and (this tree) but also (is in), forming the conceptual sequence (this cat)(is in)(this tree). In this case, this kind of sequence is caused by the manipulative features of the experienced environment and the attention we give to them. These features force the activations of certain cognitive structures that in turn bring these conceptual representations about. Of course, spoken and written sentences can also bring such sequences about. We take note of some special points.
(1) Many of our thoughts are extemporaneous combinations. In the present example, the adjunction of the different thoughts (this cat), (this tree), (is in), is a combination that is brought about not by the activation of a single, permanent, complex, conceptual structure but by the individual activations of different concepts. These thoughts form a fleeting sequence that terminates with the next movement of our thoughts, and in the absence of similar sensory or verbal prompts, the cognitive system is not likely to ever think these thoughts again. We discuss extemporaneous thinking in more detail below.
(2) Relational thoughts join conceptual representations that have different references, and such thoughts are normally not capable of adjunction. Specifically, since cats are not trees, the thoughts (cat) and (tree) are normally not adjoined.(25) However, through the employment of a relational concept an adjunction of sorts can be accomplished. The concepts (cat) and (is in) are adjoined in one way, and the concepts (is in) and (tree) are adjoined in another way, forming a three-fold adjunction.
(3) Relational thoughts are not always extemporaneous. One may expect that when similar adjunctions occur on a number of occasions, and when some cognitive significance is attached to such adjunctions, certain permanent connections will be formed among the affected concepts, resulting in the formation of standing, complex relational concepts. In this way we come to have complemented relational concepts. For example, (nourishing) is (produces)(health), (violinist) is (plays)(violin), (conductor) is (conducts)(orchestra), (drives) is (controls) (movements) (of)(some vehicle), and so on.
We give, then, the following analysis: A relational conceptual structure consists of two (or more) relay nodes connected to a cognitive structure that forms their definition. As with other concepts, the relay nodes of a relational conceptual structure form the relational concept. A concept defined by a relational structure can often be expressed in language using expressions that are converses of each other, as in "the cat is in the tree" and "the tree contains the cat." We take this to indicate not so much a difference in relational concepts as a difference in the employment of the relational concept. If the conceptual episode is focused on the cat, the relational concept will be expressed as "is in," whereas, if the episode is focused on the tree, the concept will be expressed as "contains." Some examples of relational concepts, often named by verbs with prepositions, are: (is in) or (contains), (speaks to) or (is spoken to by), (sees) or (is seen by), (is larger than) or (is smaller than), (gives to) or (receives from), and others that do not have natural converses such as (comes from), (falls into), etc.
Let us consider again the simple concept (is in). This is a simple relation of content and containment. We suppose in general that the definition of a simple relational concept is a relational feature unit {P1P2#}, and in the present example, the relational feature unit may be a structure that is some geometric composition of an inner part within an outer part. The part P1 connects to a relay node
 x ),
x ), y ). The entire conceptual structure is:
y ). The entire conceptual structure is:
(The relay node (x )—{P1P2#}—(
y ).
 x ) may be naturally thought of as the concept (is in)—(
x ) may be naturally thought of as the concept (is in)—( y ) , and the relay node
y ) , and the relay node  y )
y )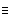 x ). Figure 6 illustrates these relations.
x ). Figure 6 illustrates these relations.
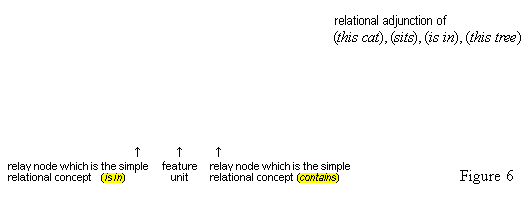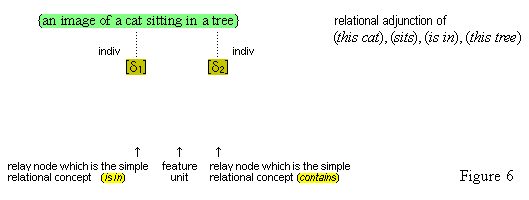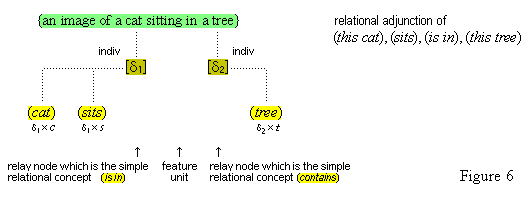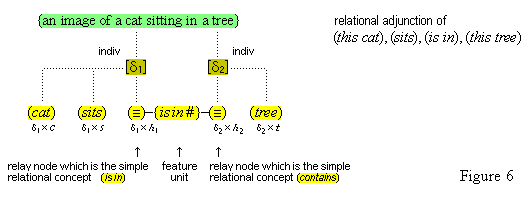
Our speculation that concepts have natural characteristic activation patterns extends to relational concepts as well. And since simple relational conceptual structures are defined by feature units {P1P2#}, with parts that distinguish the relay nodes connected to them, it is plausible to suppose that these parts also are characterized by activation patterns, h1 and h2, which are conferred on these connected relay nodes. The adjunction of thoughts employing a relational concept will, therefore, have a more complex superposition of activation patterns. If the activation patterns of (cat), (sits), (tree), (is in) are c, s, t, h1+h2, respectively, and if the activation patterns of the pointers are d1 and d2, then we speculate that the activation pattern of the thought (this sitting cat) (is in) (this tree) is:
d1×c + d1×s + d1×h1 + d2×h2 + d2×t, that is, d1×(c + s + h1) + d2×(h2 + t).§18. Transferred Adjunction.
We shall say that an adjunction of some representations is transferred when it arises as a result of the combination of other adjunctions. This is a situation of concurrent representations, where X and Y are adjoined through one connection, and Y and Z are adjoined through another connection, and where X and Z are adjoined as a result of this. Such transference is not remarkable when the adjunctions all derive from a common source, as in the case of a sensory representation of a green pen that is adjoined with a feature representation {green#}, that is in turn adjoined with the conceptual representation (green). But it is remarkable when the adjunctions derive from different sources, such as from an item of sensory perception and from an item of speech, since thoughts like that are usually merely concurrent and not adjoined.
Consider the case where Smith and Jones are looking at an old green pen, and Smith says, "That is priceless," and Jones puzzles why that is so. Somehow Jones came to think the thought (that green pen is priceless), even though he only saw the green pen and only heard the words. Transitions such as these are common, and we take them for granted. But what is their explanation? How can one explain the mysterious transition that occurs when two wholly different types of thoughts, with distinct subjects, (one originating with a visual impression, and the other originating with an auditory impression), are blended into a single thought with a single subject? The explanatory framework we have been presenting provides such an explanation, and we would suggest that without such a framework such matters cannot be explained.
We are able to give the following account. (1) The sensory representation of the pen is adjoined through individuation to an individuative pointer node [d]. (2) Through the usual conceptual connections that derive through perception, the conceptual representations (pen) and (green) are adjoined to [d] as well. (3) The node [d] is verbally adjoined with the word "that". (4) Finally, the utterance "that is priceless" causes the conceptual correlates of the words "that" and "priceless" to be adjoined, that is, causes the pointer [d] and the conceptual representation (priceless) to be adjoined. We discuss such propositional adjunction in detail below. The net result is the adjunction of the four thoughts [d], (green), (pen), and (priceless). We note in passing that transferred adjunction is a very efficient mechanism for introducing new connections in our thinking, that otherwise would not have been made. Figure 7 illustrates the matter.
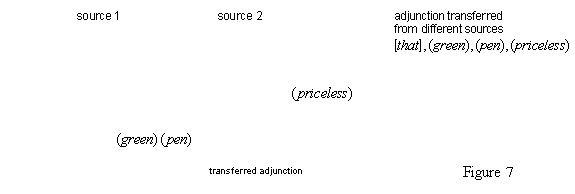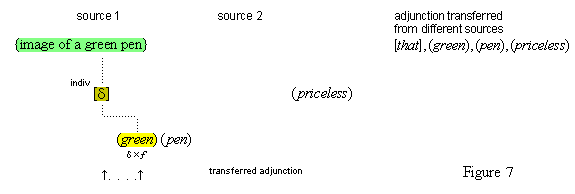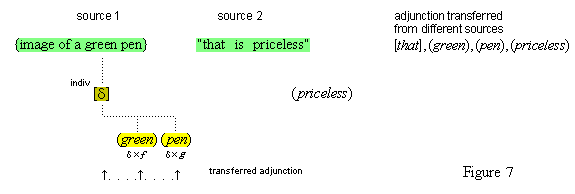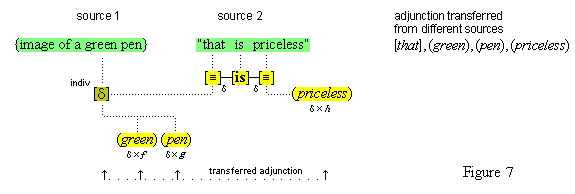
§19. Strong connection.
Much of our thinking arises from connections that were previously learned from various correlations found in our experience. (We include under this heading connections learned through education and other authoritative sources). We call these connections strong conceptual connections. The patterns of our experience naturally lead certain conceptual structures to be permanently connected with others. The conceptual adjunctions that are caused by these connections, when they occur, are automatic and forceful. We hear a certain heavy siren, and we think (fire engine) and (fire). We smell a certain aroma, and we think (baking of bread). We enter a dark room, and we think (light switch). We see steam rising from a cup, and we think (very hot). We see a white covering on the ground, and we think (snow). We see something red and shaped like an apple, and we think (apple). These are all bold movements of thought. For example, the transition from (apple-shaped) to (apple) is a considerable leap, since to think the latter is to think not only (apple-shaped) but also what cannot be seen, (edible), (fruit), (nourishing), and (food). These adjunctions are cognitive leaps, but leaps indispensable for our well-being. Figure 8 illustrates these connections.
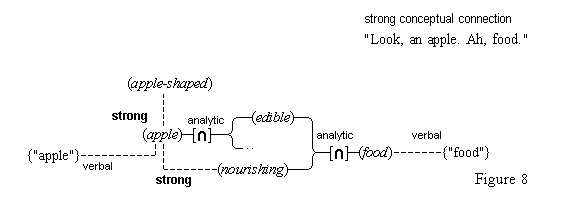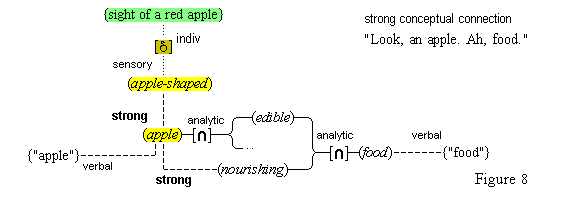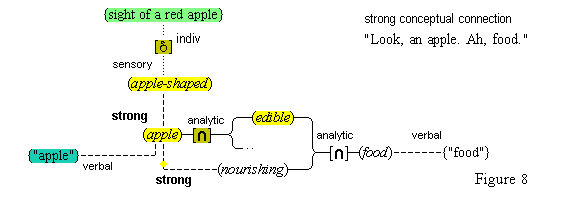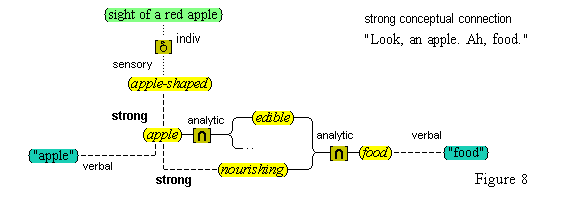
Quine on analyticity. Our account makes a firm distinction between analytic and strong connections. Quine is well-known for his attack on the notion of analyticity, arguing that there is, in principle, not a distinction between sentences that are analytically true and ones that are empirically true.(26) Given Quine's linguistic preoccupation, (shared by many), he rejects outright any traditional account of concepts and their composition, considering instead the function and use of public words and sentences. One can understand Quine's consequent negative assessment. Public words have meanings that are indeterminate to a certain extent and changeable, and it is indeed difficult to consider criteria for analyticity in such a context. But present-day cognitive science has warmly embraced conceptual representations, and considerations of language have taken something of a back seat. Our own account puts concepts and their active representations in center stage. On this account, concepts are not indeterminate, since they have definitions, in the sense we have explained above. They are also not alterable, in as much as they are permanent cognitive structures, once they exist. Word meanings, on the other hand, can change. Such a change occurs when a word becomes verbally connected, in the usual manner, with another concept, in addition to the concept whose connection constituted its original meaning. The result is a word that has a number of distinct meanings, which is a situation we are very well used to.(27) So, Quine's attack is directed at a philosophical view regarding the meaning of public words, a meaning that is indeterminate to an extent and changeable. His analysis does not consider the possibility of cognitive structures and their relations, and thus, it cannot refute our claim that analytic conceptual connections and strong conceptual connections are significantly different kinds of causal relations.
Analytic connections and strong connections are alike in the respect that they each provide a sequence of connected concepts in which the activation of the first member brings about the activation of the second. If one thinks (elephant), then through an analytic connection one thinks (elephant-shaped) (animal), and through a strong connection one thinks (eats vegetation). These sequences are similar in the sense that they are both causal relations. But there are significant differences, arising first of all from what concepts are, and secondly from the kinds of causal relations that are involved.(28)
A concept is a relay node for a structure that by default is then its definition. Thinking the relay node and thinking the definitional structure are causally the same event. Since a concept is a relay node, a concept has various connections to other nodes, and in this way it gives the cognitive system access to various types of information. But there is a criterion by which other nodes become connected with a relay node, namely, a conformity to the definition of the relay node. For example, an iconic memory of some elephant-experience becomes connected with a conceptual node N because N's definitional components, (elephant-shaped)(animal), were activated during that earlier elephant experience, as we discuss in the next section. Again, the concept (eats vegetation) becomes strongly connected with N because on several occasions when the definitional components were thought, (eats vegetation) was then also thought, that is, on account of the correlations of experience. Given, then, that definitions have this criterial role, we conclude that strong connections are extra, peripheral connections, that may, or may not, come to be formed, depending only on the accidental course of our experience, while analytic connections constitute the very existence of the concept.
A second difference involves the types of causal connections that are involved. Our theory proposes, and the evidence of introspection confirms, that we are unable to avoid thinking the components of the analytic connections embedded in our cognitive system. We are unable to avoid thinking (animal) when we think (elephant), and (container) when we think (cup). Our earlier speculations about concepts having a characteristic activation pattern can shed some light on this. If it is true that the complex activation pattern of the concept (elephant) is nothing more than the pattern that results from the superposition of the activation patterns of certain other patterns, which together are thus considered its definition, then the thought (elephant) in the literal sense contains the thought (animal) as a part, in the same way that the complex sound wave of the musical chord C major contains the sound waves of the notes C, E, and G; namely, without exactly those components, the complex wave just would be something other than the chord C major.
But, strong connections are not like that. When we perceive an apple-shaped object, we analytically think (apple-shaped), and generally, by strong connection, (apple). But not always. If we think that the apple-shaped object is wax, we think (wax apple-shaped object), and we are not led to think (apple). Again, when we think (apple), we generally think (nourishing). But if we think (poisoned apple), we think (apple) but do not think (nourishing). Likewise, we can avoid thinking of fires that they are painful, and of a badly cut hand that it will bleed. We can avoid thinking the associate of any strong connection, if we try, or are forced to. The reason for this is that strong connections are sensitive to the conceptual context at hand: they normally come into play, but they are countermanded in certain circumstances.
We can model this situation by supposing that a concept's strong connections are peripheral connections, so that thinking the concept does not constitute thinking the strong correlate, even though it may lead to thinking it. This would mean, then, that these peripheral strong connections are synaptic connections that have separate activation patterns, so that the activations of strong correlates come about by brute activation only, if at all. But one may expect that the brute activations of neural nodes are subject to the competing influences brought by the activations of the other nodes that are connected to them, since brute activations require transmissions that are sufficiently strong to overcome the activation-thresholds of the nodes being activated. This kind of circumstance makes it possible that certain activations will not succeed when there are competing activations.
And to this we may add a more theoretical consideration. It is plausible that (1) forceful activation patterns will inhibit all other incompatible activation patterns, and that (2) if some component of an activation pattern is inhibited, then that pattern is inhibited as well, since patterns are nothing more than their components. These relationships can explain how the thought of (poisoned) inhibits the thought of (nourishing), even in the presence of the thought (apple). The activation pattern of (poisoned) analytically contains the activation pattern of (produces) (non-health), and the activation pattern of (produces)(health) is incompatible with that, so that the activation pattern of (poisoned) inhibits the pattern of (produces)(health) as well as those that are analytically related, here, (nourishing) and (food). In this way, the peripheral strong connection from (apple) to (nourishing) is inhibited in the presence of other thoughts, such as (poisoned). Figure 9 illustrates this situation.
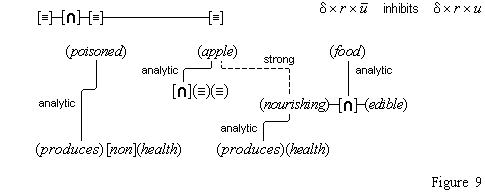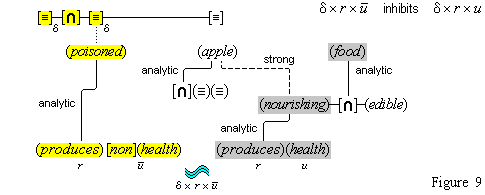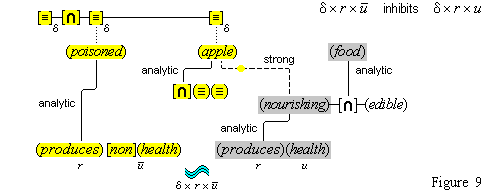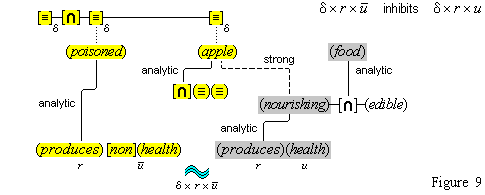
Propositional strong connection. There is another distinction to be made, one between simple connections and propositional connections. The cognitive system stores some of its information through simple links between two cognitive structures, as in the analytic link between (mother) and (female parent), or the verbal link between {"apple"} and (apple), or the strong link between (apple) and (nourishing). The cognitive system also stores some of its information in the form of sequences that are syntactically structured. We discuss this kind of connection below under the topic of propositional adjunction, so we will not try to analyze it here. When we think (the Moon), we can think (it orbits the Earth), (some people landed on it), (oxygen does not exist on it), (its surface is a desert), (we have some rocks from it), and so on. These thoughts indicate that conceptual structures, such as (the Moon), are in some instances connected to propositional sequences. We illustrate this in Figure 10.
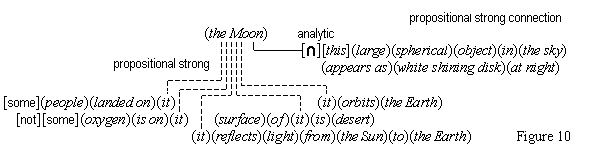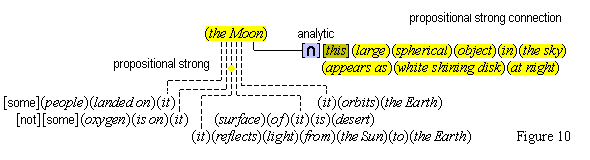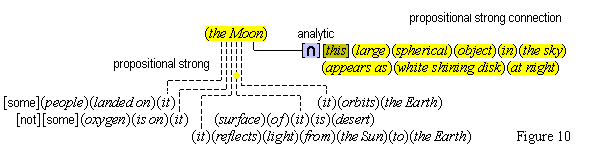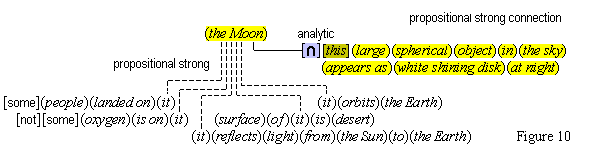
§20. Iconic memory connection.
We all have some kind of memory of the experiences that we have had. We are all able to recall things, events, scenes, situations that we have experienced, in a special way that involves mental imagery. With appropriate prompts, we can relive rather elaborate scenes of animated activity, and what must be closely related, we have no difficulty imagining the scenery and events of narratives we are told. We shall call this kind of memory iconic memory, and we shall assume that it consists of items stored in the form of iconic memory units.(29) One interesting fact about this kind of memory is that it can be activated both by our present experience and also by our present thoughts. This happy coincidence requires some explanation. Another fact regarding memory is that the number of iconic memory units must be enormous, encompassing experiences from a great part of our lives. And this magnitude presents a sorting problem, of how and which items are to be retrieved.
These matters suggest an explanation in terms of concepts. We propose that iconic memory units are directly connected to concepts, and only to them. So, only processes that engage concepts can, through them, elicit iconic memories. So, this explains why both sensory experiences and conceptual thoughts elicit iconic memory: conceptual thoughts do, and sensory experiences do because they bring about conceptual thoughts. Also, the retrieval of memories is highly selective, which we may infer from the fact that what we remember is typically very focused and very appropriate for the matter at hand. When we see an elephant, we are not reminded of the last time we had a Banana Split. This selectivity, again, suggests the intervention of conceptual thoughts. Hearing the word "elephant" activates the concept (elephant), which in turn activates one or several elephant memories, because they are connected to that concept. Likewise, when we visit a zoo, the experience may leads us to think (elephant) and so bring about our elephant memories. This explanation requires that iconic memory units are connected to concepts, with the result that when we think certain ideas, we remember certain experiences.
The question remains how iconic memory units come to be connected to concepts. Even though a great deal is known about how neurons function biochemically within the brain, very little is known about how neurons encode information. But we have seen some clues. As we experience certain events, we also think certain conceptual thoughts, that is, at the time that sensory experiences occur, a number of concepts befitting them are activated. So, it is plausible that when a memory is made of some experience, there is a double recording of both sensory and conceptual information.(30) The mechanism of memory that encodes the information of a sensory experience into an iconic memory unit also encodes, in some way, the information of what concepts were active during the experience.
Here our earlier proposal that concepts have an characteristic activation wave pattern has an immediate application. First of all, in sensory experience, sensory nodes are active with their own activation wave patterns, and that kind of activity can be recorded in a complex wave pattern. Secondly, when concepts are active, during sensory experience, with their characteristic activation wave patterns, then that kind of activity can be recorded in a complex wave pattern as well.
Perhaps this is the full extent of the connection there is, since a double encoding process can by itself explain, to some extent, how the activation of concepts is causally sufficient for the activation iconic memories. If it is true that information is encoded in iconic memory units regarding what concepts were active during an experience, then the later activation of those concepts may activate that encoded conceptual information, and in the process activate the entire iconic memory unit. More speculatively, if the encoded information were a record of some doubly complex activation pattern, of the superimposition of the conceptual activation patterns active during an experience, (it need not be one of the entire conceptorium), as well as of the complex sensory activation pattern constituting the experience, then the later activation of some of those concepts would bring about a complex activation pattern that resonates to some degree with the stored iconic pattern, and the iconic unit would thereby be activated. Such a causal relation, that is based on permanent structural similarity, is appropriately considered a kind of connection. (One may even speculate that activations brought about by resonance could eventually lead to the growth of synaptic connections.)
Propositional iconic memory.
Someone aks, "What happened when Sarah arrived at the office," and we respond with an elaborate account. The activation of this memory is a complex process. It begins with a verbal prompt that activates the concepts (Sarah), (arrived), (at the office), and continues with the activation of iconic memory that brings to mind a surprising amount of detail. Part of the detail is an experience of mental imagery, and part of it is present conceptual thought that describes this imagery: (she was nervous), (she was wearing a blue coat), (she was two hours late), (Tom was waiting), (he was drinking coffee), (the mug once belonged to Elvis), (Tom was worried about Sarah), and so on. Perhaps some of these thoughts are not themselves memories, but are thoughts newly formed on the occasion of entertaining the memory. Such thoughts could perhaps arise in much the same way that thoughts arise when we are engaged in normal sensory perception. But some of these conceptual thoughts must themselves be memories, since they involve information that cannot be stored in, nor retrieved from, mental imagery. An image of a cup containing a liquid cannot contain as sensory information that the liquid is coffee, nor that the cup once belonged to Elvis. So, in addition to sensory information, memories must store some kind of conceptual information, in virtue of which we are later able to think (he was drinking coffee) and (the mug once belonged to Elvis) when the memories are activated.
More involved is the matter that some of the conceptual accompaniments of memory are syntactically structured. As we remember the event about Sarah, we think the syntactically structured propositions: (she was wearing a blue coat), (Tom was worried about Sarah), (he was drinking coffee), (the mug once belonged to Elvis). Again, some such propositions may be extemporaneously composed on the occasion of remembering the event. But some propositions involve arrangements of ideas, as in (the mug once belonged to Elvis). Since syntactic arrangements are the kinds of things that cannot be encoded as images, they must be separately encoded. So, we conclude that in addition to a store of sensory information, iconic memory units also contain a store of conceptual information, some of which is simple and some of which is syntactically structured.
Considerations of the conceptual and propositional content of memories strongly support a double encoding of information. Iconic memory units store not only sensory information which is later re-experienced, but store as well conceptual information which is later re-thought. The fact that we remember some propositional content that cannot be part of the stored sensory information, proves that some double encoding takes place. It is a small concession to say that all conceptualization of a focused experience is encoded in a memory. A model of stored activation patterns can accommodate both types of information: a complex sensory activation pattern is superimposed with a concurrent complex conceptual activation pattern, and the resulting complex activation pattern of sensory and conceptual information is stored in an iconic memory unit. When such a unit is later activated, we re-experience and re-think an earlier event.
§21. The weakness of strong connection.
It must be allowed that not everything we have learned from experience has the same kind of immediacy in our thoughts. We know much about cars, houses, animals, electronic devices, and so on, that is available when prompted for in some way, but that is not ordinarily present in our thoughts, or at least in our conscious thoughts. What happens when someone hears the word "apple" and thinks (Adam and Eve)? There must, of course, be some kind of link between these items, presumably, in this case, arising from a remembered narrative. But that does not explain why the thinking did not proceed to (Snow White), or (William Tell), or (grocery store), which also have some link. Why do some links produce a result, and not others?
One would expect that the cognitive system must be selective in what it thinks, since we are noticeably very limited with respect to how much information we can process at any given time. This would mean that the cognitive system must not be forced to process irrelevant information on account of connections that have an automatic and immediate effect. For example, when the traffic light turns red, we must not be diverted from our stop by a forced contemplation of the correctness of traffic laws, or of the engineering aspects of traffic control, or of the influence of certain colors on the actions of some animals – all of which have some connection to the thought (the traffic light turned red). This consideration suggests that the cognitive sytem must be, and is, so designed that at any given time some of its connections have their effect and others not.
The answer to our query must therefore be found in the nature of synaptic connections and the activations they allow. We discussed this matter earlier in section 2, and we noted that the existence of a synaptic connection between two neural nodes does not guarantee that activation of the first will bring about the activation of the second. It is true that some synaptic connections seem to be very strong, and the transfer of activation seems to be guaranteed. For example, whenever we see flames near us, we always think that they can burn us. This fear of flames requires that there be a strong connection between the concepts (flame) and (it burns you when touched). Again, whenever we hear a proper "meow" sound, we always think (cat), in virtue of the latter's strong connection with the concept (meow). Nevertheless, all strong connections are inherently weak.
Every neural node has an activation threshold, which is a certain level of electrochemical input the node must endure in order to be activated. (Such a threshold could arise not only from the activation thresholds of the individual neurons that constitute the node but also from the number of these neurons and the manner in which they are interconnected.) The existence of a threshold means that if a node receives transmissions that collectively exceed the activation threshold, the node will be activated, but not otherwise. Note that low transmissions do not prevent the receiving node from being made active to some degree. Indeed, in order for thresholds to be exceeded, every transmission that a node receives must endow the node with some degree of activity, which is added to the activity bestowed by other transmissions.
Here then is part of the answer to the question of how the cognitive system is able to select certain connections rather than others in its thoughts. In many cases, a single concept has several strong connections to different concepts, as in the connection of (cat) to (meows), (drinks milk), (climbs trees), (has fur), (purrs), (dislikes dogs), (eats mice), and so on. Yet, the activation of that concept does not lead to the activation of all the strongly connected concepts, as may be easily observed in the case when someone hears the word "cat" but does not think (climbs trees). What this means is that, for the most part, strong connections generate a level of transmission that is lower than the activation threshold of any of the connected nodes. If we set the activation threshold of concepts generally to be 1.00 activation units (AU), then we may suppose the transmission level of strong connections to be less than that, say, 0.90 AU. So, the activation of the concept (cat) gives a transmission input of 0.90 AU to the concept (climbs trees), which is not enough to activate it. But if the node (climbs trees) also receives a concurrent transmission from another node, say from the concept (climbs) or (tree), the two transmissions will combine to exceed the activation threshold of (climbs trees) and will thus fully activate it. In this way only those thoughts will be selected that have a special significance, that is, that are supported by more than one source. And, to return to the original example, perhaps it was a present preoccupation with the concept (sin) that led one to think (Adam and Eve sinned when they ate the forbidden apple in the garden of Eden) upon hearing the word "apple."
And so, the other part of the answer regarding selectivity comes from the situation of prompting. (The paradigm case of prompting comes from theatrical productions where an actor has forgotten his lines and someone off-stage must whisper a word or two to get the actor back on track.) With respect to the activation of concepts this phenomenon consists of a concept that first receives a below-threshold activation input from one source, and next receives another below-threshold activation input from another source, such that the combined input is one above the activation threshold. Hearing the word "cat" provides an activation charge of 0.90 AU to many concepts, including (climbs trees). Likewise, hearing the word "climbs" provides an activation charge of 0.90 AU to many concepts, including again (climbs trees). Hearing these two words together, therefore, provides the concept (climbs trees) with an activation charge that is above the threshold, causing us to think and say "climbs trees". Figure 10b illustrates the process of activations with strong connections.
One may perform some easy tests that tend to confirm these proposals: The subject is to report what comes to mind when certain words are heard. One is able to observe that a single word gets a hesitant and varying response, whereas pairs or triplets of words tend to get a direct and consistent response.
| spoken words | activated concepts | result | strong connections |
| "cat, sound" | (cat), (sound) | (meows) | (cat) (meows) (meows) (sound) (sound) |
| "cat, drinks" | (cat), (drinks) | (milk) | (cat) (drinks milk) (drinks milk) (drinks) (drinks) |
| "cat, climbs" | (cat), (climbs) | (tree) | (cat) (climbs tree) (climbs tree) (climbs) (climbs) |
| "cat, soft" | (cat), (soft) | (fur) | (cat) (has fur) (has fur) (soft) (soft) |
| "cat, happy" | (cat), (happy) | (purrs) | (cat) (purrs) (purrs) (happy) (happy) |
| "cat, fears, animal" | (cat), (fears), (animal) | (dog) | (cat) (fears)–(dog) (fears)–(dog)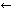 (animal) (animal) |
| "cat, umbrella" | (cat), (umbrella) | (huh?) |
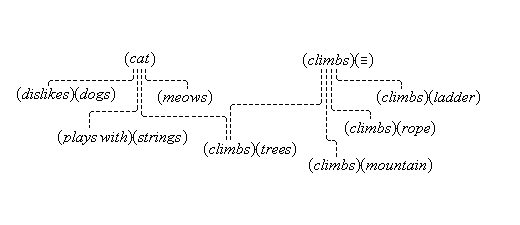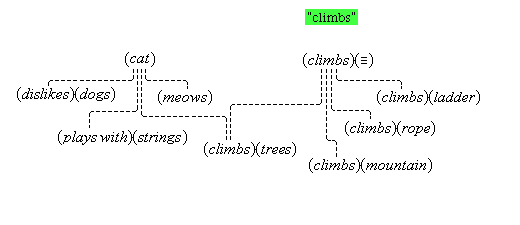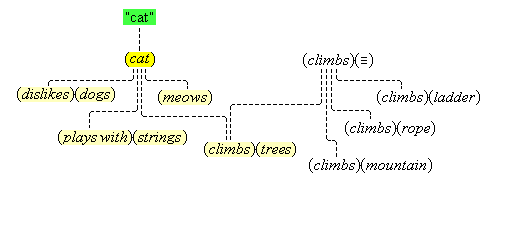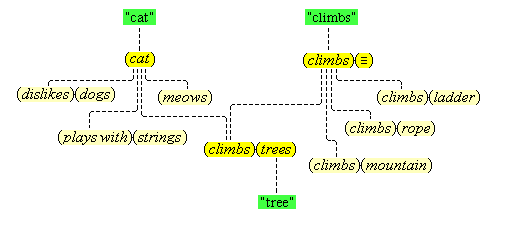
Figure 10b
The ideas we have presented here regarding strong connections agree to a significant extent with the views proposed by connectionist theories: (1) all nodes have an activation threshold, (2) at any given time, all nodes have a certain accumulation of activation input determined by the transmissions received at that time from all their connected nodes, and (3) connections among nodes have varying degrees of strength. The most important difference between our view and standard connectionist theories is that we take each concept to have a definition, that ultimately resolves into some special content that characterizes that concept and that determines its characteristic activation pattern, which pattern when active constitutes the thought we are engaged in. By contrast, connectionist theories reject the existence of such definitions and such special content. All connections are strong connections, distinguished only by their number and their arrangements within the system. Inputs to the cognitive system generate a present system-state of activation in virtue of existing connections. The only "activation pattern" recognized in connectionist theories is the distribution of the accumulated activation inputs that all the nodes happen to have at that given moment.
§22. Extemporaneous conceptualizations.
Regarding our active thoughts, there are two kinds of complex conceptual representations. One kind consists of the adjoined thoughts that are brought about by the activation of a single, standing, complex concept, such as the adjoined thoughts (edible) and (nourishing) when we think the concept (food). The second kind consists of the adjoined thoughts that are brought about by the activations of distinct concepts that have no connection other than a present, temporary link caused by perception or speech, such as the thoughts occasioned by the sight of a cat running across the yard, or by the phrase "telephone area code for the Moon." In the one kind of conceptualization, one thinks a single complex concept (together with those concepts that are analytical contained in it); and in the other kind, one thinks a collection of otherwise unconnected concepts that have become temporarily linked. We call the latter extemporaneous conceptualizations.
We can discern two main sources that lead to extemporaneous conceptualization. (1) One source is sensory perception. With little exception, our sensory perceptions are far too complex to be represented by a single complex concept. Rather, in sensory perception a number of different and unconnected concepts are activated and adjoined. We see a fluffy kitten wearing a blue ribbon sitting in a tree with no leaves, and we think [this](fluffy)(kitten), (it wears), [this](blue)(ribbon), (it sits), (it is in), [this](tree), (it has no leaves). This conceptualization is not the activation of a ready-made concept; it is rather an extemporaneous conceptualization.
(2) A second source is speech, the sequences of words that we hear or see written, or that we say silently to ourselves. The phrase "telephone area code for the Moon" elicits the different thoughts (telephone area code), (is for), and (the Moon), that are temporarily linked into a relational adjunction. Some futurists may indeed have a complex concept that meets this description, but for most of us the arrangement is quite extemporaneous. These conceptualizations can, of course, lead to the creation of concepts. Indeed, we may speculate that today some of us have begun to acquire the concept (telephone area code for the Moon), since today we had such a thought.
(3) As to other sources, philosophers have traditionally attributed the ability to combine concepts to an ability referred to as the power of imagination. It is not clear whether this ability is intended to cover cases beyond those of sensory perception and speech, say, cases of special creativity, through which some concepts just come to be temporarily (and perhaps randomly) linked. We certainly do not rule out the possibility of such, and even other, sources of conceptualization. But however that may be, the distinction between standing and extemporaneous conceptualizations obtains.
We want to stress the importance of the difference between concepts and extemporaneous conceptualizations. It is not uncommon for philosophers to hold that verbal descriptions define concepts. This has the result that all such descriptions are taken to stand for concepts. Somewhat along these lines, Fodor says that "a concept is what an open sentence of a natural language expresses," and gives the phrase "lives in Chicago and eats mangleworts" as an example of a phrase that expresses a concept.(32) Views such as these, that mistake certain possible extemporaneous conceptualizations for concepts, have some very unpalatable consequences. (1) On such a view, every open sentence of the natural language, expresses a concept. But this would fabricate an enormous collection of conceptual entities, such as Fodor's example above, for which there is no evidence that they exist. Since the set of open sentences of a language is infinite, the set of concepts of the speakers of the language would also have to be infinite. But consider: the number of neurons that exist is finite, and the number of simple distributed neuron groups is finite, and the number of connections that exist at any time among neuron groups is finite. At any given time, therefore, the number of concepts is also finite. What are left over are the infinitely many possible and actual conceptualizations that are not concepts at that time, and perhaps never will be. (2) Since all speakers of the language are able to produce any open sentence, on such a view, all speakers of the language possess all concepts. The Pilgrims, then, who came over on the Mayflower in 1620, would actually have had the concepts of electricity, gasoline powered automobiles, and atomic fission, without, of course, realizing they had them, and without employing them. But one must simply insist here that those who hold this theory are not talking about concepts. They are not talking about what people think, nor are they talking about the structures that characterize people's minds. We conclude, then, that the failure to distinguish between concepts and extemporaneous conceptualizations is a plain theoretical error. Figure 11 illustrates the connections in extemporaneous conceptualization. (We discuss formal structures in the following section.)
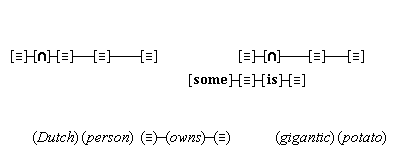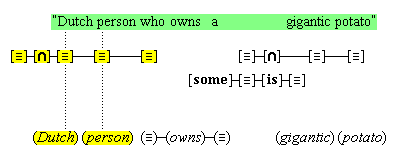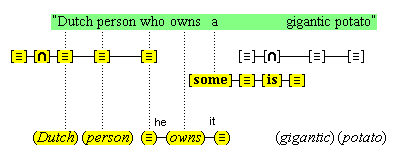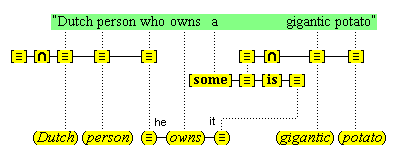

§23. Propositional adjunction.
The most apparent connections in our thoughts are found when we are engaged in speech. Their presence is evident, but they are difficult to explain. We see something, and we immediately give a verbal report, as if we were just reading off a ready-made description. Or, we hear someone say something, and we immediately give an elaborate response, again, as if we were just reading off a ready-made answer. Our words just seem to come to us, and they can even surprise us, with regret or satisfaction. So, what enables us to do this? We venture the answer that, in fact, we are just reading off a ready-made description.
Our framework commits us to an analysis whose basic terms are cognitive nodes and their active representations. The traditional analysis of language has always proposed that (1) our words express concepts, (while most phrases do not), and that (2) our sentences express propositions that are composed of those concepts. Sentences are special sequences of words that have a surface-level grammatical structure, and they express propositions that have a corresponding lower-level construction composed of corresponding concepts and operations. We follow this traditional analysis, except that we also take concepts and propositions to be cognitive structures composed of neurons.
An important fact about propositions is that they must be created instantaneously as we think them, and they must cease to exist (except for our memory of some of them) when we stop thinking them. We understand the never before encountered sentence, "some elephants are yellow telephones," as soon as we engage it; that is to say, we immediately think the corresponding proposition. But we cannot suppose that such propositions exist prior to their evocation in thought, since the number of possible propositions is infinite, while the total number of neural items in existence is finite. So, propositions must be newly generated in our minds whenever they are considered. For this purpose, the cognitive system has at its disposal a large number of simple and complex concepts, including relational concepts and quasi-concepts. We now also propose that the system has a modest number of very simple cognitive structures, multiply duplicated, that are formal simple predication structures, such as the structure
[≡]—[is]—[≡], or more intuitively, [it]—[is]—[such] .These structures have an inherent function with dedicated nodes that are free connection points, to which concepts and other formal structures are temporarily connected and then released. When such connections occur, the result is an extemporaneously connected sequence of cognitive structures that constitutes a proposition. For example, when the concepts (the Moon) and (round) are temporarily connected to the free nodes in [≡]—[is]—[≡] , the proposition (the Moon)[is](round) is formed:
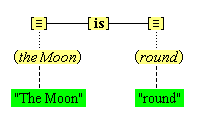
As this sequence is activated, we come to think the proposition, and in virtue of the simple verbal connections that concepts have with word patterns, we come to think a sentence as well, which we may or may not express out loud. When the activation ceases, the extemporaneous connections cease to exist, and the proposition dissolves into a collection of inactive, and unconnected, and unrelated items.
Each formal simple predication structure consists of an operator node [is] together with some variable nodes that are synaptically connected to the structure.(33) Presently we will concern ourselves with individual variable nodes,
With respect to how formal structures become activated, we distinguish two kinds of processes: downward processing and upward processing. (1) In downward processing there is a process that begins with speech (heard spoken or seen written) and that continues with certain formal structures being recruited and activated, and certain concepts being linked and activated, and an active thought being produced. For example, when we hear the sentence "Chicago is a city", a formal structure [≡]—[is]—[≡] is recruited and activated, and the concepts (Chicago) and (city) are linked to its indivual variables and activated, and an active thought deriving from the activation wave patterns of these concepts is then produced. (2) In upward processing, the sequence is reversed. The process begins with certain concepts being active, it continues with certain formal structures being recruited and activated, and it ends with certain sentences being produced. For example, when the concepts (Abe Lincoln) and (tall) have been activated in such a way that the reference value d is linked with each, the formal structure [≡]—[is]—[≡] is recruited and activated, and the two concepts are linked thereto, so that the proposition (Abe Lincoln)··· [≡]—[is]—[≡] ···(tall) is generated, and the sentence "Abe Lincoln is tall" is thought.
We will discuss propositions in two stages. Here and in section 25 we discuss simple propositions, and in section 28 we discuss compound propositions. Compound propositions, as we will later discuss, are built up from simple propositions by means of special propositional operators, that are altogether different from the conceptual operators we considered above. Simple propositions lack propositional operators, but they make liberal use of conceptual operators to generate their subjects and predicates.
§24. Combinatorial conceptual structures.
Earlier in section 13 we introduced three groups of conceptual operator nodes, namely, the negative operator nodes [non], the conjunctive operator nodes [∩], and the potentive operator nodes [can]. These nodes are multiply duplicated, so that similar operator nodes can occur in different places within a single proposition or in other simultaneously produced propositions. It is time now to have a closer look at these operators, because they are the items that are responsible for the complex structure and content that the subject and predicate variables [≡] of a predication structure can have. We note that we are here considering the extemporaneous use of these operators within the system rather than the use we considered earlier in the formation of permanent complex concepts.
Structure #1. The negative conceptual operator, [≡]—[non]—[≡] . This structure distributes an inherited reference value d to both variables, and further associates with the operator variable an activation wave pattern F×a that is the opposite of the activation wave pattern a linked with the operand variable. Both patterns are modified by the reference value d. We use a bold-faced symbol F to denote this negative modification of the wave pattern. We note that negation-modification does not distribute over addition, whereas reference-modification does. As an example, the next linked structure is the extemporaneous conceptualization (non-singing), and produces the fleeting thought d×F×s, which is an activation wave pattern that contains both a blocked (or diminished) contribution by the base concept as well as the full-force information generated by the negative operator.
Structure #2. The conjunctive conceptual operator, [≡]—[∩]—[≡]—[≡] . This structure inherits a reference value d, and all activation wave patterns modified by this reference value are linked with the variable nodes according to the following condition:
the operator variable takes on the modified superimposed wave pattern d×a + d×b if and only if the two operand variables are linked with concepts that have the modified activation wave patterns d×a and d×bFor example, the spoken phrase "yellow telephone" produces the linked structure indicated below, which is the extemporaneous conceptualization (yellow telephone), that produces the fleeting thought d×y + d×t while active.
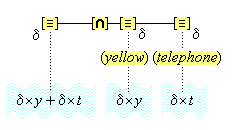
Structure #3. The potentive conceptual operator, [≡]—[can]—[≡] . This structure distributes an inherited reference value d to both variables, and further associates with the operator variable an activation wave pattern P×a that is the potentive modification of the activation wave pattern a linked with the operand variable. Both patterns are further modified by the reference value d of the variables. Again, we use the bold-faced symbol for potentive-modification to distinguish it from reference-modification. For example, the linked structure
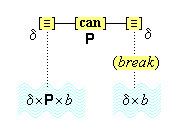
is the extemporaneous conceptualization (breakable), producing the fleeting thought d×P×b as long as the structure is active. Again, we must assume that the presence of the potentive operation diminishes (or blocks) the activation wave pattern of the base concept.
The following figure illustrates an extemporaneous conceptualization that combines the three combinatorial operators.
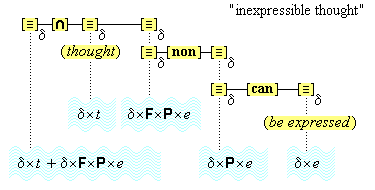
§25. Predication structures.
In addition to the three merely combinatorial conceptual structures, there are also three formal predication structures that have specific propositions as their instances. Each predication structure has two variable components, one that acts as the subject and another that acts as the predicate. The distinction between subject and predicate is not merely grammatical. The function of a proposition is to make information about the subject that is implicitly contained in the system explicitly available to other processes, such as public speech.
Structure #4. The simple predication structure, [≡]—[is]—[≡]. This structure has the function of propositional predication, and is expressed in our language by the verb "is", as well as by any verb phrase whatsoever.(33) The first variable node acts as the subject of the structure, and the second variable node acts as the predicate. When the variables are linked with concepts, a proposition is formed, and when this structure is activated, a momentary propositional thought occurs with an activation wave pattern determined by the components.
The subject variable and the predicate variable have reference values that are inherited in system processes. In downward processing, whenever the predication structure [≡]—[is]—[≡] becomes activated, the reference value of the subject variable is transferred to the predicate variable.The activation wave patterns linked with these variables are modified by the reference value that the variables have, and the activation wave pattern for the entire proposition is the result of their superimposed combination. For example, he proposition (Sam walks), i.e., (Sam)[is](walks), has the following configuration:
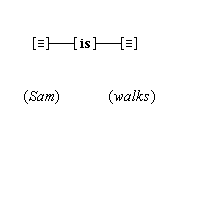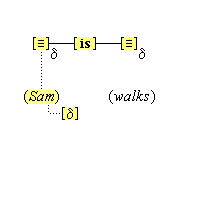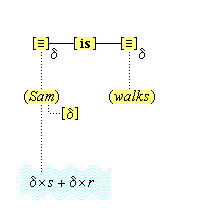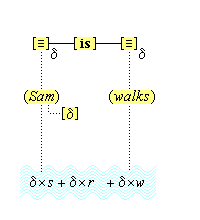
Activation stages for a
simple predication structure
There are distinct stages that characterize the activation of a simple predication structure, beginning with the application of reference value and ending with the generation of an activation wave pattern for the proposition created by the structure.
Predication structures also have an important evaluation function discussed in section 27.
Structure #5. The existential predication structure, [some]—[≡]—[is]—[≡]. As in the previous case, the existential structure also has the function of propositional predication, and is also expressed by any verb phrase. The first variable node functions as the subject of the structure, and the second variable node as the predicate. When these variables are linked with concepts, a proposition is formed, and when this structure is active, a thought occurs with an activation wave pattern determined by the components. This structure is special in that it can generate new reference values:
Whenever the existential structure becomes activated, this structure generates and distributes to both the subject and predicate variables a new reference value d, i.e., a value that is not already present in the system.When an existential structure introduces a new reference value into the system, what happens is that we begin to think about an unspecified thing, distinct from all other things we have thought about. We think that it has the properties given by the concepts associated with the subject and predicate variable, but because this is a new reference value, we do not have any prior information specifically about it. On the other hand, the subject concept will have general information in virtue of the analytic and strong connections that belong to the concept, and the predicate concept may be able to prompt the activation of certain strong connections in the subject. For example,
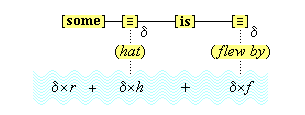
This is the proposition (some hat flew by), that is, [some](hat)[is](flew by). The reference item is [d]. The subject concept (hat) together with the predicate concept (flew by) can prompt the activation of the conceptualization (will drop when wind stops) and perhaps more. These additional thoughts have the pattern d×r , so that the proposition has the activation wave pattern d×r + d×h + d×f . A dynamic illustration of another existential predication is given in Figure 12.
Like the simple predication structure, the existential predication structure has an evaluation function that we shall discuss in section 27.
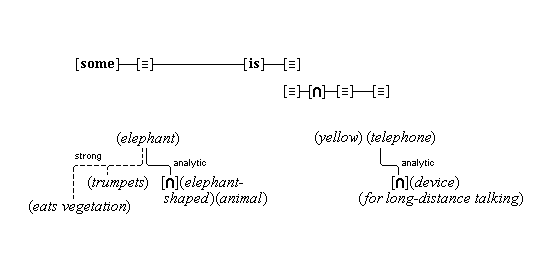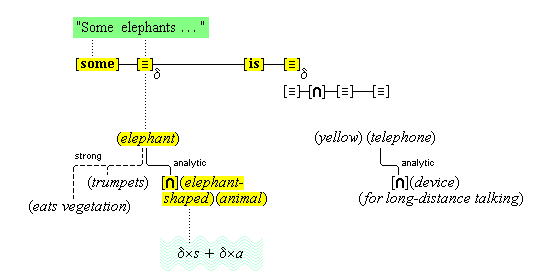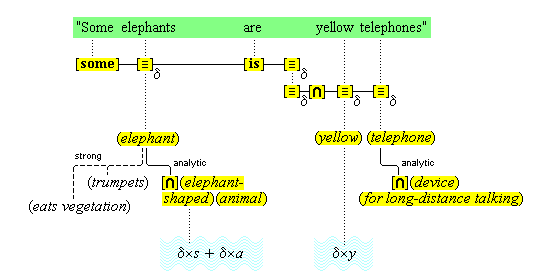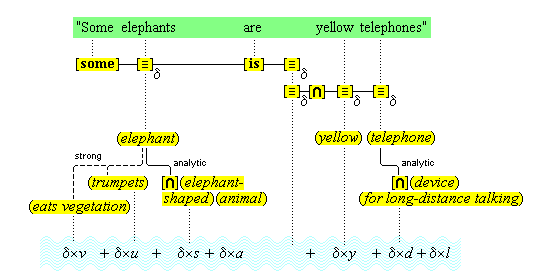 Figure 12
Figure 12
Structure #6. The universal predication structure, [all]—[≡]—[is]—[≡] . As in the two previous cases, this structure has the function of propositional predication, and is also expressed by any verb phrase. The first variable node functions as the subject of the structure, and the second variable node functions as the predicate. When the subject node and the predicate node are linked with concepts, a proposition is formed, and when this structure is activated, a thought occurs with an activation wave pattern determined by the components. Reference values in a universal predication structure are distributed in a special way:
Sequencing arises in downward processing when a concept, such as (cat), has acquired different reference values, d1 and d2 , as in (this cat), (that cat). If we now also think (all cats are aloof), the distinct reference values associated with (cat) will be sequentially transferred to (aloof). Again, the activation wave patterns linked with the subject and predicate are modified by the active reference value, and the activation wave pattern for the present thought is the result of their superimposed combination. The following linked structures illustrates such sequencing for the proposition [all](cat)[is](aloof):
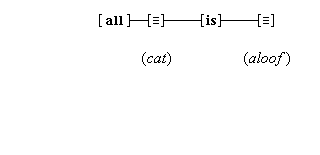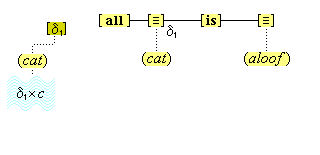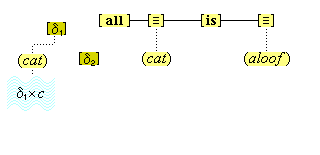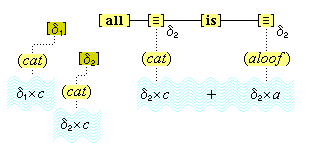
First, the proposition [all](cat)[is](aloof) is thought. The subject is the concept (cat), and the predicate is the concept (aloof). The subject next acquires the reference value d1 when a certain cat is thought of. This value is then transferred to the predicate. Thus the active thought d1×c becomes the thought d1×c + d1×a. Then another cat comes into view, causing the thought d2×c. Since the proposition [all](cat)[is](aloof) is still active, the subject and predicate take on the reference value d2. Thus, the thought d2×c becomes the thought d2×c + d2×a.
Another illustration of universal activation is given in Figure 12b, for the proposition (all tigers are dangerous). Notice how in this case the predicate activation wave is part of the subject activation wave. This kind of agreement between the subject and the predicate plays the central role in the evaluation of this thought.
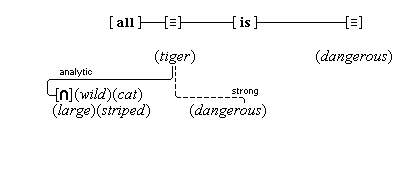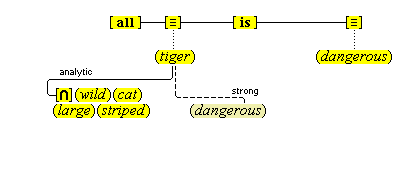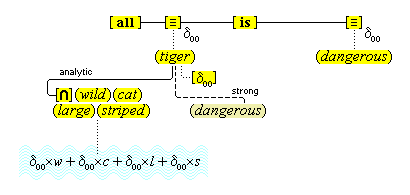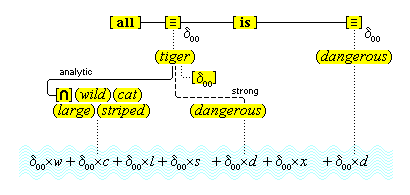
Figure 12b
As in the case of the other predication structures, the universal predication structure also has an evaluation function that we shall discuss in section 27.
Negative predication structures. Our speech and our thoughts seem to utilize negative predication structures and propositions:
The question that arises is whether such structures are original in the system or whether they are derivative combinations of other structures that together function as negative predications. There is good reason to think that these structures are in fact derivative combinations, and that they are permanent combinations rather than extemporaneous ones. The combination would be one that joins the affirmative predication structure [≡]—[is]—[≡] to the negative operator [≡]—[non]—[≡] . Given our earlier analysis of the negative operator [non], this would require that negative predication structures have their predicate variable modified by the negative value F when they are activated, in the manner that we have discussed this value earlier. We illlustrate the situation for the above proposition about the Moon. (Note the permanent connection between the two structures.) We will discuss in later sections how affirmative and negative predications are evaluated in opposite ways.
[≡]—[is not]—[≡] (the Moon)[is not](planet) [some]—[≡]—[is not]—[≡] [some](birds)[is not](winged) [all]—[≡]—[is not]—[≡] [all](dogs)[is not](cats)
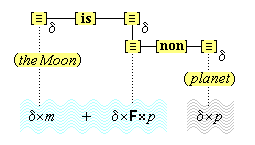
Summary. The three combinatorial structures and the three predication structures, all multiply duplicated permanent fixtures, and the propositional operators to be discussed shortly — these items constitute a formal grammar at the deepest possible level of the cognitive system.(34) These structures can be temporarily linked with each other, but also they are linked with other cognitive structures that have a content, namely, individuative pointers, concepts, quasi-concepts, and extemporaneous conceptualizations, that together may be called semantical structures. In a literal sense, then, these formal and semantical structures together form the much sought-after Language of Thought.(35)
§26. Evaluating simple predications.
There is a difference between thinking something and judging it to be true (or false). For example, we can think that Chicago is an elephant, in the sense of having that thought; and when we do, we judge it to be false. These activities are in part accessible to our introspection: we are aware of our thoughts and judgments. We have up to this point concerned ourselves with an analysis of the various elements that are part of thinking. We now add to this foundation an analysis of the process of judging propositions to be true or false.
Thinking a proposition. When we hear (or see written) the sentence "Chicago is a city," the conceptual associates of the words cause the extemporaneous formation and activation of the proposition
(Chicago) ··· d [≡]—[is]—[≡] d ··· (city), or just, (Chicago)[is](city)in the manner we have discussed above. The activation of this proposition further brings about a propositional representation, the active thought itself, consisting of the superposition of two wave patterns: the pattern d×h, brought about by the activation of the concept (Chicago), which includes an individuative pointer [d] that creates the reference value d, and the pattern d×c, brought about by the activation of the concept (city). The superposition is the pattern:
d×h + d×c.Of course, the concept (Chicago) is a complex concept, having the components (city), (in Illinois), (on the edge of Lake Michigan), (has 4 million people), etc.; and it is the activation wave patterns of these components that make up the activation wave pattern h . Likewise, the concept (city) is a complex concept, having the components (place), (large group of people live there), (has streets), (has houses), (has businesses), etc. So, the activation wave pattern produced by the entire proposition includes the sum of the parts of h and of c :
d×( a1 + . . . + an ) + d×( b1 + . . . + bm ), that is,We make a further distinction. The subject not only contains those concepts that are analytically connected, it also typically has many strong connections, as well as many iconic memory connections. Yet, unlike the analytic connections, the strong and iconic memory connections must typically be prompted for before they become active in our thoughts. For example, when we think of one person, say Grandma, the concepts (Grandma) and(person) are activated, but we do not think all the items that are connected with these concepts: our iconic memories associated with (Grandma) are not activated unless some item prompts us to think them. Does Grandma sing? That recollection had to be prompted for -- here, by the very question posed. Normally, some such prompting for additions to the subject of a proposition is provided by the concurrent activation of the concepts of the predicate of the proposition itself — a very convenient and efficient circumstance. This means, then, that the subject activation wave pattern has a dynamic size and content. As we think more intently about the subject, its wave pattern grows larger as more strong components are activated, or it changes with a partially different content as different memories come into play. But the analytic components of the subject are always present. Even more complicated cases can arise when there are additional independent sources of conceptual content, namely, the concurrent extemporaneous conceptualizations generated by present sensory perceptions or other speech. We can give a more precise characterization of this extended subject activation wave pattern:
( d×a1 + . . . + d×an ) + ( d×b1 + . . . + d×bm )
(ii) In the presence of other processes of the system, the activation wave pattern d×a is reinforced with all the other d-modified activation wave patterns present in the system, those being d×u1 , . . . , d×uk , some of which already existed prior to d×a , some of which are caused by d×a , some of which are caused by still other sources such as perception and speech, and some of which are caused by some combination of any of these sources.
(iii) The dynamically larger activation wave pattern so associated with d×a is
( d×a1 + . . . + d×an ) + ( d×u1 + . . . + d×uk )
We will refer to this combined wave pattern as the extended activation wave pattern for d×a , or just, EXT(d×a) .
(iv) The entire activation wave pattern produced on the occasion of thinking the entire proposition at issue takes the following form:
| EXT(d×a) | + d×b |
| given subject + added subject related components | + predicate |
| ( d×a1 + . . . + d×an ) + ( d×u1 + . . . + d×uk ) | + ( d×b1 + . . . + d×bm ) |
It is important to consider that the total activation wave pattern of a proposition develops and grows in distinct stages. First the given subject is activated. Next in line are the added activations of associated subject components, including those associated subject components, if any, prompted for by the predicate. We may suppose that the extented subject has sufficient opportunity to superimpose all these components to form a stable activation wave pattern. To all of this is subsequently added the activation wave pattern of the predicate. This last addition is special, because the very superposition of the predicate wave onto the extended subject wave provides an inherent comparison of these two waves. Is there an increased resonance, indicating truth? Is there a noticeable dissonance, indicating falsehood? Or, does neither of these occur, indicating ignorance? We pursue this kind of evaluation in the discussion that follows.
Evaluating a proposition. Once a proposition has been extemporaneously constructed, it is available for a special process that we may call evaluation. We propose that the actions that we usually refer to as realizing something, or making a judgment, or coming to a conclusion, or making an assertion, all involve a basic and automatic evaluation process. Sometimes we get so caught up in the process that we find ourselves exclaiming (even if silently to ourselves) "Yes!", "That's it!", "No!", "Wrong!", "Well,...", "Uh,...," and so on. But more generally, the realizations, judgments, conclusions, or assertions are made without fanfare, and pass as unnoticed parts of our many daily routines. In sum, it is a plausible hypothesis that whenever a proposition is formed, an evaluation procedure is initiated, and we may even consider this to be an automatic continuation of the process that forms the proposition. The procedure is mostly an unconscious one, but at times it becomes deliberate. Sometimes the procedure comes to a decisive result, but it is often unresolved. (Of course, any process can always be interrupted or preempted by some other process.) The following figure gives a summary of the evaluation process, that we will now analyze and illustrate.
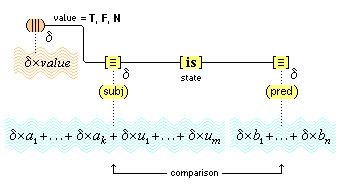
comparison of subject to predicate *
agreement
disagreement
indifference
TRUE in the system
FALSE in the system
NULL in the system
* for affirmative predicates
We propose that the simple predication structure [≡]—[is]—[≡] has a double function. It is (1) a syntactical structure that joins a subject and a predicate node into a proposition. That much is obvious. But we propose that it is also (2) a semantical operator that determines whether the predicated relationship of the proposition is correct or not, relative to the information contained in the cognitive system. This second function is perhaps best viewed as a by-product of the fact that concepts have activation wave patterns. The grammatical function is always (inherently) in force, and the semantical function is normally operative as well.
The simple predication structure [≡]—[is]—[≡] performs a passive comparison procedure on the concepts that form its subject and predicate, and depending on the comparison state that results, the entire proposition receives a value that represents the comparison. This situation requires that propositions have a propositional variable node (|||) that acts as a buffer that can hold the output value of the comparison procedure and that can also act as a connection point to other propositions. They are thus structures
These structures employ a passive comparison procedure in the following sense: Predication structures through their temporary link to the subject and predicate concepts are sensitive to an agreement or disagreement of the predicate activation wave pattern with the examined, extended subject activation wave pattern. We do not have to postulate a big logic machine here, because the kind of detection required here can be a very simple, primitive process, such as the superposition of two waves. When the individual variables of a predication structure are temporarily linked with a subject and a predicate, the activation wave patterns of the subject and predicate are likewise temporarily linked with those individual variables, as illustrated in the figure. The resulting superposition can then deposit an output in the "value buffer" (|||) attached to the predication structure. So, given the linkage that a predication structure has with the respective activation wave patterns, the predication structure is able to receive a truth-value from the passive comparison that naturally occurs between the wave patterns. We consider three cases of comparison and the consequent outcomes.
Definitions. Let d×g and d×h be any two activation wave patterns modified by the reference value d that are active in the system. (We presuppose here our earlier discussion of what superimposed wave patterns are, how the identity of their parts is preserved in the superposition, and how some wave patterns are modified by the negative value F.)
Comparisons. In the three cases that follow, the predicate activation wave pattern, such as d×b , is compared with the extended subject activation wave pattern, such as EXT(d×a) .
Case 1. There is an agreement; specifically, the predicate wave pattern agrees with the extended subject wave pattern, in the sense that the predicate wave pattern is already present in, that is, is a part of, the extended subject wave pattern, because the predicate in its entirety repeats a part of the subject. This situation, because of superposition, will produce an increase in resonance, something easily detectable in the system. So, this is a case in which the information stored under the subject contains the information of the predicate, and here we find ourselves saying "Yes!" We propose that this comparison state produces a certain affirmative output in the propositional variable (|||) that belongs to the predication structure and that is dedicated for this purpose. This is a value production that we introspectively experience as a feeling of acceptance or agreement, and that we refer to here as assigning the value TRUE to the proposition. Consider again our earlier example,
(|||)—(Chicago)[is](city)
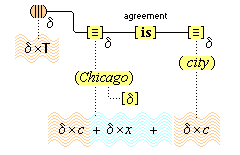
Since the concept (city) is itself an analytic part of the concept (Chicago), the activation wave pattern for the subject (Chicago) is d×c + d×x , where d×x is the wave pattern sum of the other components of (Chicago). And thus, the activation wave pattern of the subject completely contains the activation wave pattern d×c of the predicate (city). This is a case of agreement, and the evaluation process sets the propositional variable at the value TRUE.
Consider also the following example. Here the value of the proposition does not depend on an analytic relation, but rather on a remembered fact. A question about whether Grandma can sing prompts us to recall a birthday event at which Grandma did sing. The proposition
(|||)—(Grandma)[is](can sing)is then evaluated in the following way. We noted above earlier that iconic memory units record both sensory and conceptual information. They also have only strong connections (not analytic ones) with other concepts, so that memories must always be selected through an additonal secondary prompt. So, as the individual concept (Grandma) is activated, together with the prompting concept (sing), a memory unit is activated, with an attached individuative pointer [d] that is an item of reference in the system with the associated conceptual content of Grandma singing at the birthday party. This pointer thus activates the concept (can sing), and the activation wave pattern d×s is added to the extended subject activation wave pattern, resulting in
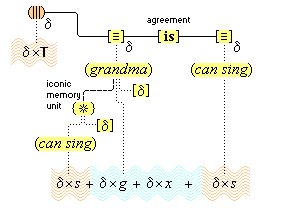
Case 2. There is a disagreement; specifically, the predicate wave pattern disagrees with the extended subject wave pattern, in the sense that the predicate wave pattern in whole or in part is the opposite of some part of the extended subject wave pattern. We may suppose that the superposition of two opposite waves produce a certain dissonance, something that is easily detectable in the system. This comparison state produces a certain negative output in the propositional variable (|||) that belongs to the predication structure, that we introspectively experience as a feeling of rejection or disagreement, and that we refer to here as assigning the value FALSE to the proposition. Consider the proposition
(|||)—(Chicago)[is](elephant)
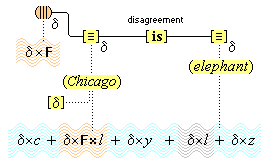
This is a case of multiple disagreements, but only one is required. The predicate has several concepts, (elephant-shaped), (living), (sentient), (self-moving), each of which disagrees with the subject. In particular, the subject contains the concept (city), and some remainder, and analytically includes the concept (non-living). So, here the predicate contains the component (living), with a pattern d×l , and the subject contains the component (non-living), with the opposite pattern d×F×l , which is a case of disagreement. The evaluation process sets the propositional variable at the value FALSE.
Case 3. There is neither agreement nor disagreement. We call this a case of indifference. The predicate contains something other than what the subject provides, so that there no agreement; but the predicate does not contradict the subject, so that there is also no disagreement. In this situation there is no resonance in the superposition, nor is there a dissonance, and this indifference is something that can be detected in the system. This comparison state produces an output of indeterminacy in the propositional variable (|||) that belongs to the predication structure, that we introspectively experience as a feeling of indeterminacy or don't know, and that we refer to here as assigning the value NULL to the proposition. Consider the proposition
(|||)—(Abe Lincoln)[is](stamp collector)Let us say that d×x + d×y + d×z is the wave pattern for (Abe Lincoln), and that d×u + d×v + d×w is the wave pattern for (stamp collector), where all these components are unrelated to each other. We have here:

Here, the wave pattern for (stamp collector) is not a part of the extended subject activation wave pattern, so that there is no agreement, and no part of the wave pattern for (stamp collector) is the opposite of any part of the extended subject activation wave pattern, so that there is no disagreement. When there is neither agreement nor disagreement, the evaluation process sets the propositional variable at the value NULL. How different this situation would be for someone else who had, for some peculiar reason, a belief that Abraham Lincoln was in fact stamp collector. Always, the values being generated for propositions are particular to the cognitve system that contains them.
§27. Evaluating existential and universal predication structures.
Admittedly, so far we have presented only simple examples. Now the account becomes more complicated. Some of these complications come from the semantical side, involving the sources used in the evaluation process, and other complications come from the syntactical side, with more complicated grammatical constructions. Existential and universal predication structures have a double complexity. Not only is there a predication relation between the subject and the predicate that requires a comparison, there is also a stipulation of the quantity of positive outcomes for such comparisons.
So, with respect to these quantifies, we must consider the various items of reference that are contained in the system for our active concepts. The individuative pointers of sensory experience provide items of reference [d] , and the units of iconic memory about specific things provide items of reference [d] . In addition, assertions of speech provide items of reference [d] , as when someone reports, "An elephant tried to get into a rowboat." These items are the reference values that are used for the subject-predicate comparisons mandated by the quantifiers. Existential predications require that at least one comparison is positive, and universal predications require that all comparisons are positive. From introspective reflection we know that this evaluation process can be an imprecise activity, sometimes quick and easy, sometimes quite labored, and sometimes unreliable. ("Oops, forgot about that one.")
It is not clear how many of these comparisons the system is able to make at the same time. Can there be many simultaneous, pair-wise, wave pattern comparisons? Specifically, can all the following predicate-to-subject comparisons be made at the same time?
d1×h is compared to EXT(d1×g)We have supposed that the modification that the reference values d bestow on wave patterns actually prevents any blending or confusion of wave pattern information, and so, we will also suppose that it is as easy for the system to (passively) make many simultaneous comparisons between activation wave patterns as it is to make a single comparison. We take this situation to be just another example of parallel processing in the cognitive system. (We could, of course, suppose instead that all comparisons are made sequentially, one after the other. That is a simpler scenario, but a less likely one. In both scenarios the needed comparisons are made, but simultaneous computations are obviously much more efficient: they take the time of one.)
d2×h is compared to EXT(d2×g)
d3×h is compared to EXT(d3×g)
...
We present the more complicated procedures for evaluation existential and universal predications. These procedures must first make a number of comparisons of the subject and predicate for the various reference values dj. Each such comparison produces a truth-value (called a base-value) for the item dj involved in the comparison. Thereupon, the procedure assigns a truth-value (called the end-value) to the proposition as a whole.
existential predications
[some] (
The proposition has subject (
1. Activate all reference values dj that are instances of (
Activate all the corresponding EXT(dj×a) , including all prompting results by (
2. Activate all the corresponding predicate wave patterns dj×b .
Initiate all the resonance tests.
(i) If there is a case of agreement for the value dk ,
universal predications
[all] (
The proposition has subject (
1. Activate all reference values dj that are instances of (
Activate all the corresponding EXT(dj×a) , including all prompting results by (
2. Activate all the corresponding predicate wave patterns dj×b .
Initiate all the resonance tests.
3. Result:
(i) If there is a case of disagreement for the value dk ,
Let's look at some quantified evaluations. Suppose someone asks, "Are some flowers red?" This question prompts us to think the corresponding proposition (note the two value nodes):
(|||)—[some]—(|||)—(flower)[is](red)Presumably, for most of us, the evaluation of this proposition will follow from our memories of the different kinds of flowers we have experienced (but maybe it was something we were told). Let us suppose that we have one such memory of a red flower, a rose. Let this be the iconic memory unit
 }.
}.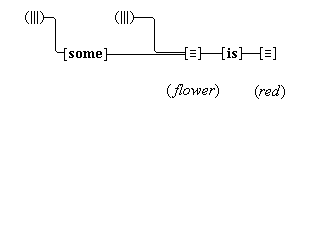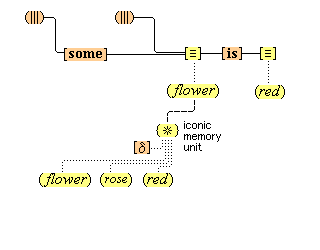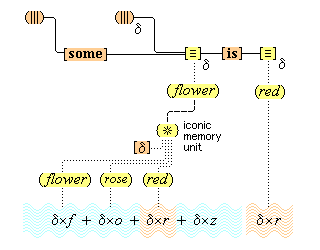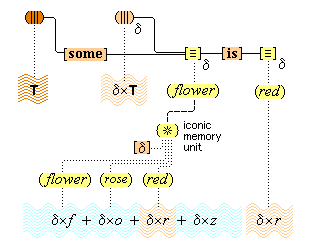
"Are some flowers red?"
A more complicated example comes from universal evaluations. Such evaluations often display our lack of knowledge; but when they are based on analytic or strong connections, the result is always affirmative. When someone asks, "Are tigers dangerous?" we are led to think the proposition
(|||)—[all](tiger)[is](dangerous).Since the concept (dangerous) is a strong component of the subject concept (tiger), and since the predicate also prompts the subject for this idea, the extented subject activation wave pattern for this proposition will always contain the activation wave pattern for the predicate concept (dangerous), for each reference value d that exists in the system. Hence, the comparison always results in agreement, so that the universal evaluation procedure always encounters the referenced value TRUE for each reference item [d]. Because of this repeated agreement, this universal proposition receives the value of TRUE.
 "Are tigers dangerous?"
"Are tigers dangerous?""Of course!"
Figure 14b
Relational sentences have a complex grammar. Not only does the predicate contain a relational concept, but the two sides of the relation also each have a quantifier. For example, the question "Do birds eat birds?" prompts us to think the proposition
(|||)—[some](bird)[is](eats)[some](bird).
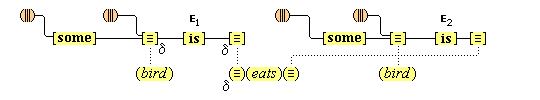
This proposition relates two quantities, and it must, therefore, contains two predication structures, E1 and E2. These thoughts also excite the memory of an eagle [δ1] eating a small bird [δ2]. Since the extented subject activation wave pattern involves both [δ1] and [δ2], this activation wave is available in the system for any quantity comparisons with respect to both [δ1] and [δ2]. This memory passively produces four affirmative judgments, as illustrated in the figure below. Let's walk through the stages.
1. The extended subject activation wave pattern for predication E1 is formed. Under prompting from the predicate, this wave pattern includes the memory content of an eagle [δ1] eating a small bird [δ2]. Thus, EXT(δ1×b) includes:
δ1×b + δ1×a + (δ1×e1 + δ2×e2) + δ2×s + δ2×b.Since the two reference values δ1 and δ2 are now both active in the system, comparisons for each of them will be passively made.
2. Next, the predicate wave for predication E1 is formed. But the predicate is itself an existential predication structure E2 , so that various extended subject activation wave patterns for E2 will passively be formed and undergo comparisons with the predicate activation wave pattern of E2.
3. As E2 cycles through all reference values, the value δ2 is also included, so that EXT(δ2×b) is formed for E2 , and this wave pattern is passively compared with the predicate wave for δ2 for E2 .
4. Specifically, EXT(δ2×b) for E2 includes all active system information, including the information active in EXT(δ1×b) for E1, and that means that EXT(δ2×b) includes the information about [δ1] eating [δ2], which is the information δ1×e1 + δ2×e2 .
5. But the predicate for δ2 in E2 is (δ1)(eats)(δ2 ), so that the predicate activation wave pattern is δ1×e1 + δ2×e2 , and consequently, the comparison for δ2 for E2 is positive.
6. And simultaneously and passively, the predication structure E1 now also detect a positive match between its own extended subject activation wave pattern and its own predicate activation wave pattern, since the latter is: δ1×e1 + δ2×e2 + δ2×b, all whose parts are included in EXT(δ1×b)
7. This positive match assigns the existential proposition the value T, as in the next figure.
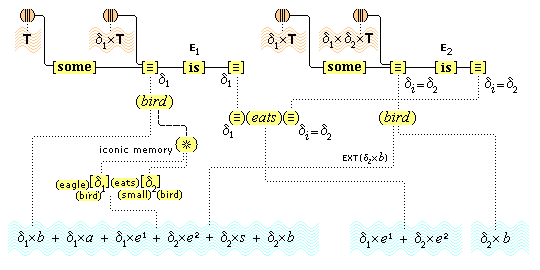
Evaluating negative predications. We proposed earlier that negative concepts are characterized by a special "negative" activation wave pattern that takes the form δ×F×a . Negative activation wave patterns are admittedly speculative formalities postulated by our theory to accommodate the idea of negation. While conjunctions are characterized in Nature by the superimposition of different waves patterns, there does not seem to be in Nature a compositional wave phenomenon that corresponds to the operation of negation.
Still, that does not mean that there is no way to accommodate negation by means of activation wave patterns. We propose that the cognitive system has some way of modifying wave patterns by some special factor F that is unique in the system in such a way that other kinds of wave pattern configurations cannot be confused with it (perhaps through a special frequency that is not otherwise used in the system). When such curious items come into existence, the only thing that matters is how the system behaves in dealing with those curious items. In particular, the only thing that matters for an activation wave pattern δ×F×a is that its consequences are the opposite of the consequences of the corresponding un-modified wave pattern δ×a .
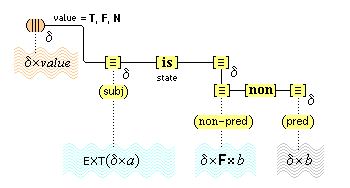
predicate is a negated structure
procedure compares the subject
and the un-negated predicate
and inverts the resulting value
If δ×b disagrees with EXT(δ×a) then value = T
If δ×b is indifferent with EXT(δ×a) then value = N
When we apply the above considerations to the evaluation process of predication structures, we can see that we can accommodate negative predicates by simply assigning truth-values that are the opposite of those assigned for the comparisons for the un-negated predicates.
Some examples will help. The first one involves a visual experience, in the context of some preoccupation. In particular, there is a visual search for something that is a box and that is also green. This is a typical case where there are several separate sources of information, but in this case, (1) a prior conceptual concern, with its concepts, and (2) a sensory experience, with additional concepts. A proposition is formed and evaluated, and perhaps it is accompanied by a verbal report.
So first, we see a red box. (See the figure below.) Thereupon, a new item of reference [δ] becomes active in the system, and it is temporarily associated with the visual sensory field. The feature unit {red#} is activated and is also temporarily associated with item [δ]. This feature unit, in turn, is analytically connected to the simple concept (red), and is also activated. In addition, the prior involvement with the concept (green) has the effect to prompt the system to test the application of (green) to [δ]. This fundamental test of applicability is based on the mechanics of color detection with color feature units. We may suppose that the color sensorium is so designed that the activation of one color feature unit for an item δ makes it causally impossible for other color feature units to be so activated. If the system at the same time then prompts for one of these causally incompatible features, we may suppose that the system will respond to such an attemp by applying the false factor, F, in this way broadcasting a strong disagreement to the rest of the system. What we have in this example, then, is that the system entertains the proposition,
(|||)—(δ)—[is]—[non]—(green)whose subject is the experienced sensory item [δ], and whose extended subject activation wave pattern includes all the observed features of [δ] as well as the negative information that the system generated when it was prompted to do so:
δ×b + δ×r + δ×F×gThe activation wave pattern for the un-negated predicate disagrees with the extented subject activation wave pattern, and this disagreement produces the value T for the negative predication structure.
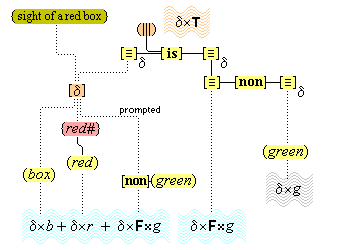 "Ah, there's a box,
"Ah, there's a box, but it's not green."
In the next example the negation is based on analytic connections. Consider the proposition, a prince is not a princess. Why the negative predication? Because, a prince is a person of royalty who is male, and a princess is a person of royalty who is not male, and these two three-membered combinations are in disagreement because a part of the one is the opposite of a part of the other. (The very same disagreement displayed here also governs the converse proposition, a princess is not a prince.) This disagreement must always exist here because of the analytic connections that each side has. So, for all reference values δ, the negative predication structure must return the value T, and the universal proposition must likewise be T.
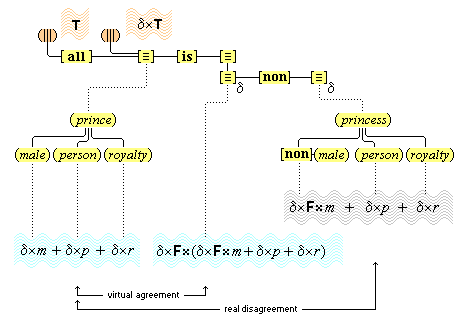
§28. Compound propositions.
We introduce now the operator nodes that form our complex propositions. We limit our discussion to the common four types of propositional operators. These are
There are important differences between propositional operator nodes and conceptual operator nodes. First of all, conceptual operator nodes operate on individual variable nodes, [≡]1 , [≡]2 ,
negative propositional operator nodes: [not]0, [not]1, [not]2, . . . ; conjunctive propositional operator nodes: [and]0, [and]1, [and]2, . . . ; disjunctive propositional operator nodes: [or]0, [or]1, [or]2, . . . ; conditional propositional operator nodes: [if]0, [if]1, [if]2, . . . .
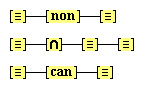
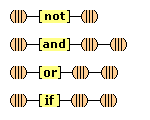
Secondly, whereas conceptual operator nodes mostly combine simple concepts into permanent complex structures, (although they also sometimes enter into extemporaneous combinations), propositional operator nodes produce only extemporaneous complexes of propositions, by means of temporary links. Complex propositions always cease to exist as soon as their temporary links are broken, as is true also of simple propositions themselves, as discussed above. A striking feature of propositional operator nodes is that, as they form their links with propositions, they combine and transform the truth-values ( T, N, F ) of those propositions. Here is an example of a compound proposition, constructed from two simple propositions by means of a negative propositional operator and a conjunctive propositional operator.
(|||)—[not]—( (|||)—[and]—((|||)—(grandma can sing))——((|||)—(grandma can dance)) )
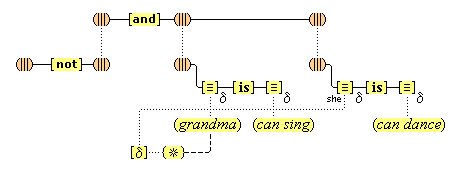
Before we present the procedures that evaluate compound propositions, we make an important distinction regarding the truth-values T, N, F. These values are reports of predication evaluations, where T indicates agreement and F indicates disagreement. The value N, however, has a curious status. It is not really a third value that rivals the other other two. The value N is a system indicator that the other two values are not available to present state of the system. The value N indicates a lack of knowledge within the system at a given point in time. But knowledge in the system grows, and what was once unknown can become T or F at a later stage. The system of human thought is a two-valued domain, but the system must also accommodate ignorance, and it does so by means of an indication that behaves macroscopically as though it were a third value N. But we should not overlook the fact that this one value represents two possible states: unknown value that is T or F. We venture to suggest that the incongruity among the values is illustrated by the fact that we have clear and immediate expectations about how the values T and F combine systematically to form expected resulting values, but we do not have any such expectations when the value N is involved (although we are able to pause and figure things out). Consider,
(1) Abe Lincoln was a President, and he also lived a long life.
(2) Abe Lincoln collected stamps, and he also lived a long life.
We immediately perceive the values of the components parts of both these propositions, and in that respect there is no difference between them, but there is a difference between the propositions as a whole. We immediate perceive that (1) as a whole is F, but the system seems to ignore (2) as a whole. And we propose that this a general reaction. When the value N is involved, the system seems to passively revert to a default state in which there is:
(i) a focus on the part that is NBut it is certainly true that the system will consider such matters more carefully when there are special factors at play in the system that prompt it to do so. We are certainly able to figure out that propositions like (2) resolve to the value F. We propose that when the system does figure it out, it employs a non-passive, special procedure that we will call the two-valued resolution procedure, that we will introduce shortly.
(ii) a broadcast of that status,
(iii) a termination of further consideration: "What's next?"
In standard logic, the evaluation procedures for the propositional operator nodes are always presented in the form of four-row truth-tables. But such descriptions do not shed light on the physical implementation of these procedures, and for that reason we favor a different type of description. Since truth-values have a physical manifestion as wave patterns, descriptions in terms of magnitudes may be physically significant, but in any event, such description are convient. We give the values T and F a magnitude with respect to each other, so that we can define the notions of a maximum value and a minimum value for a pair of values when those values are limited to just T or F. We also define an inverse opposition function that makes T and F opposites of each other. We will represent the inverse function as , using the notation of an over-line. In all this we note that none of these notions are defined for cases when the value N is involved. Since the value N represents two unknown values, the notions in question are not applicable. The relationships for the values T and F are as follows:
• value T is greater than value FThe evaluation procedures that we will present for the four propositional operators agree with, what is commonly knows as, the standard two-valued truth-functional analysis, except that we must make provision for the value N to accommodate cases of ignorance.
• for any pair containing T, T is the maximum: maximum(T, X) = T
• for any pair containing F, F is the minimum: minimum(F, X) = F
• values T and F are inverses of each other: T = F, F = T
Of course, we cannot just stipulate that the propositional operators are truth-functionally defined. How the cognitve system works is an empirical matter, and that is also true for the logic that the system uses. There have been developed a number of non-standard systems of logic in which the propositional operators are not truth-functionally defined.(36) But these system do not describe the regular reasoning used by us. All empirical indications are that our everyday thoughts are in exact agreeement with the standard two-valued truth-functional analysis. (All institutions of higher learning have for many years incorporated this fact into their academic curriculums in their teaching of standard logic.)
There are some related issues about the methods that the cognitive system uses as it reasons out its conclusions. One may ask whether there is some special type of thinking peculiar to disjunctive thinking, or to conditional thinking. For example, is there a special kind of thinking in which the one domain of thought is divided into two separate tableaux that are alternatives to one another? If there were, then that could be the basis for disjunctive thought. Again, one may ask whether there is a special kind of thinking in which the domain of thought is augmented by one additonal tableau headed by a hypothesis? If there were, then that could be the basis for conditional thought. These are genuine possibilities, but at this point we have no knowledge about these matters. Significantly, if these special kinds of thinking do exist, then we know one important thing about them: they have to be such that the propositional operators [not], [and], [or], [if] turn out to have the truth-functional behavior that we have specified here, because it is an empirical fact that our everyday thoughts are in exact agreement with that truth-functional behavior.
Here are the evaluation procedures:
ZX
 Value Z is the inverse of the value X.
Value Z is the inverse of the value X.
ZXY
 Z is the minimum of the values X and Y
Z is the minimum of the values X and Y
ZXY
 Z is the maximum of the values X and Y
Z is the maximum of the values X and Y
ZXY
 Z is the maximum of the values and Y
Z is the maximum of the values and Y
We can now show how the previous example of grandma singing and dancing is evaluated passively by the system, (provided sufficient thinking resources have been allocated). Here, we use the following abbreviations: S = Grandma can sing , D = Grandma can dance.
(value?)—[not]—((value?)—[and]—(S)—(D))
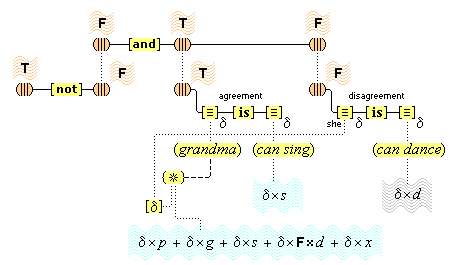
Let's consider again the example we discussed earlier,
Abe Lincoln collected stamps, and he also lived a long life.We proposed earlier that the system normally dismisses consideration of propositions that involve the value N, but that the system is able to figure out the resultant value of such propositions, if the system has been prompted to do so. We also proposed that the system employs the two-valued resolution method to make the calculations. This is a simple method that temporarily successively replaces all the indifference values that are present by the real values T and F. These various replacements generate scenarios for the compound proposition in which all the simple components have either the value T or F. In each scenario, therefore, for a sentence that involves the value N, calculations are made that involve only the values T and F. The resolution value for a compound proposition is determined in the following way:
(|||)—[and]—(N)——(F)
| Outcomes | Resolution value | |
| (a) | All the temporary scenarios result in T | the value T |
| (b) | All the temporary scenarios result in F | the value F |
| (c) | Some scenarious result in T, and some in F | the value N |
We continue with the given example:
Abe Lincoln collected stamps, and he also lived a long life.Since only the first component part has the value N, only that value needs to be expanded into the two possible cases. The second component part has a known value of F, so that value remains constant throughout, and consequently the scenarios for this resolution are the two scenarios indicated. Column [1] and [2] produce the values in column [3], using the evaluation procedure for the conjunctive operator. Finally, since all the scenarios in column [3] have the outcome F, the resultant value of the compound proposition resolves to just the value F. Here's another example, but one in which both components have the value N:
F
F
[3]T
F
[1]F
F
[2]scenario #1
scenario #2
Abe Lincoln collected stamps, and his wife did also.In this example, each component part has the value N, so in each part the value needs to be replaced by the two possible values. That means that the possible scenarios are the four scenarios indicated in columns [1] and [2]. Those two columns produce column [3], using the rule for conjunctions, and since column [3] contains some T and also some F, the resolution value for the compound sentence is the value N. Finally, our last example:
T
F
F
F
[3]T
F
T
F
[1]T
T
F
F
[2]scenario #1
scenario #2
scenario #3
scenario #4
Abe Lincoln collected stamps, or else he didn't.In this example, there is a compound sentence, but it is constructed out of a single component proposition. So, there is a single occurence of the value N that needs to be replaced by the two values. That means the scenarios for this proposition are the two scenarios indicated in column [1]. This column produces column [2], using the rule for negations. Column [3] repeat the values of column [1] since those two columns represent the same sentence. Columns [2] and [3] then produce column 4, using the rule for disjunctions. Since all the values in column [4] are T, the resolution value for this compound is the value T.
T
T
[4]T
F
[3]F
T
[2]T
F
[1]scenario #1
scenario #2
So, in all three examples, there are components that have the value N, and in all three cases, the resolution procedure generated a final resolution value. We add here that the results produced by the resolution procedure agree entirely with an independent, intuitive estimate of what the values should be. We take this to be good evidence for the existence of resolution method in the cognitive system.
§29. Conformity of our conceptualist theory with standard logic.
The conceptualistic analysis of propositional thinking that we have presented here has the important result that all the standard principles of logical reasoning are preserved under this analysis. When propositions are analyzed in the manner we propose, the principles of logic are derivable as causal processes that operate with necessity within the cognitive system. This is not a trivial result. We have given propositions an extraordinary analysis, in which propositions are constructed out of unusual objects that behave in unusual ways, and in which truth and falsehood is a function of comparisons. That such an extraordinary account is capable of generating the principles of logic is therefore a significant item of evidence, one that gives strong support for the theory that we have presented.
We demonstrate the conformity in question for four important groups of logical principles: (1) valid categorical syllogisms, (2) the well-known quantifier-negation laws, (3) rules for propositional inference, and (4) logical tautologies. We begin by re-listing the definitions we made earlier, followed by some useful theorems:
Definitions. Let δ×g and δ×h be any two activation wave patterns, modified by the reference value δ, that are active in the system.
Theorem 1. If δ×f agrees with EXT(δ×g), then EXT(δ×f) = EXT(δ×g)
Proof:
|
1. δ×f agrees with EXT(δ×g) 2. δ×f is part of (the sum of all the active patterns δ×uk ) + δ×g 3. δ×f, and δ×g, and all the other δ×uk is the list of active patterns. 4. EXT(δ×f) and EXT(δ×g) have the same active patterns. 5. EXT(δ×f) = EXT(δ×g). |
Hypothesis From 1, by def. 1, 5 From 2 From 3, by def. 5 From 4 |
Theorem 2. If δ×f agrees with EXT(δ×g), and δ×g agrees with EXT(δ×h),
then δ×f agrees with EXT(δ×h)
Proof:
|
1. δ×f agrees with EXT(δ×g) 2. δ×g agrees with EXT(δ×h) 3. EXT(δ×g) = EXT(δ×h) 4. δ×f agrees with EXT(δ×h) |
Hypothesis Hypothesis From 2, by Thm. 1 From 1, 3 |
Theorem 3. If δ×f disagrees with EXT(δ×g), and δ×g agrees with EXT(δ×h),
then δ×f disagrees with EXT(δ×h)
Proof:
|
1. δ×f disagrees with EXT(δ×g) 2. δ×g agrees with EXT(δ×h) 3. EXT(δ×g) = EXT(δ×h) 4. δ×f disagrees with EXT(δ×h) |
Hypothesis Hypothesis From 2, by Thm. 1 From 1, 3 |
Group 1. Conformity with valid categorical syllogisms. We have in mind such valid patterns as:
|
All A are B All B are C All A are C |
Some A are B All B are C some A are C |
All A are B No B are C No A are C |
and a number of other similar patterns. According to our theory these patterns are generated by certain configurations of various kinds of connected nodes, and are subject to certain evaluation processes. Without displaying all of these nodes and connections in detail, we may adequately represent the listed patterns in the following manner:
|
(T)—[all]( (T)—[all]( (T)—[all]( |
(T)—[some]( (T)—[all]( (T)—[some]( |
(T)—[all]( (T)—[all]( (T)—[all]( |
We will focus on just these three, and we leave it to the reader to verify that all other valid syllogisms can be demonstrated in similar fashion. To show that these nodal configurations conform to their logical counterparts, we will show that they are system-valid, in the sense that whenever the system renders the premisses as having the value T, the system must also render the conclusion as having the value T. (The necessity of any causal process is qualified only by system malfunction due to external forces.) We let a, b, and c, be the activation wave patterns of the concepts (
| i. |
1. (T)—[all]( 2. (T)—[all]( 3. for all refs δ for ( 4. for all refs δ for ( 5. for all refs δ for ( 6. (T)—[all]( |
Hypothesis Hypothesis From 1, evaluation From 2, evaluation From 4, 3, theorem 2 From 5, evaluation |
| ii. |
1. (T)—[some]( 2. (T)—[all]( 3. for all refs δ for ( 4. some ref δ° for ( 5. δ° ref for ( 6. δ° ref for ( 7. for some ref δ for ( 8. (T)—[some]( |
Hypothesis Hypothesis From 2, evaluation From 1, evaluation From 4, 3, instantiation From 5, 4, theorem 2 From 6, generalization From 7, evaluation |
| iii. |
1. (T)—[all]( 2. (T)—[all]( 3. for all refs δ for ( 4. for all refs δ for ( 5. for all refs δ for ( 6. (T)—[all]( |
Hypothesis Hypothesis From 1, evaluation From 2, evaluation From 4, 3, theorem 3 From 5, evaluation |
Group 2. Conformity with the quantifier-negation laws. These laws are the following relationships, where "
 " denotes that the two sides are logically equivalent expressions:
" denotes that the two sides are logically equivalent expressions:
These equivalence patterns correspond to the following nodal configurations:
Again, to show that these nodal configurations conform to their logical counterparts, we will show that they are system-equivalent, in the sense that whenever the system renders either side of the correlation as having the value T, the system must also render the other side of the correlation as having the value T. (The necessity of this causal process is qualified only by system malfunction.)
| i. |
1. (T)—[not][all]( 2. (F)—[all]( 3. some ref δ for ( 4. (T)—[some]( |
Hypothesis, one of the sides 1 = 2, neg. prop. evaluation 2 = 3, quant. evaluation 3 = 4, neg. pred. evaluation |
| ii. |
1. (T)—[not][some]( 2. (F)—[some]( 3. for all ref δ for ( 4. (T)—[all]( |
Hypothesis, one of the sides 1 = 2, neg. prop. evaluation 2 = 3, quant. evaluation 3 = 4, neg. pred. evaluation |
| iii. |
1. (T)—[all]( 2. for all ref δ for ( 3. (F)—[some]( 4. (T)—[not][some]( |
Hypothesis, one of the sides 1 = 2, quant. evaluation 2 = 3, neg. pred. evaluation 3 = 4, neg. prop. evaluation |
| iv. |
1. (T)—[some]( 2. some ref δ for ( 3. (F)—[all]( 4. (T)—[not][all]( |
Hypothesis, one of the sides 1 = 2, quant. evaluation 2 = 3, neg. pred. evaluation 3 = 4, neg. prop. evaluation |
Group 3. Conformity with the rules of inference for compound propositions. We have in mind such valid patterns as:
| disjunctive syllogism P or Q not P Q |
the rule modus tollens if P then Q not Q not P |
hypothetical syllogism if P then Q if Q then R if P then R |
the double negation law not (not P) P |
DeMorgan's equivalence not both P and Q not P or not Q |
and a number of other well-known laws of propositonal logic. According to our theory these patterns are generated by certain configurations of various kinds of connected nodes, and are subject to certain evaluation processes. Without displaying all of these nodes and connections in detail, we may adequately represent the listed patterns in the following manner:
|
(T)–[or]( (T)–[not]( (T)–( |
(T)–[if]( (T)–[not]( (T)–[not]( |
(T)–[if]( (T)–[if]( (T)–[if]( |
(T)–[not][not]( (T)–( |
(T)–[not][and]( (T)–[or][not]( |
We will focus on just these five, and we leave it to the reader to verify that the other laws of propositional logic can be demonstrated in similar fashion. To show that these nodal configurations conform to their logical counterparts, we will show that they are system-valid, in the sense that whenever the system renders the premisses as having the value T, the system must also render the conclusion as having the value T. A note about the notation below: for convenience of display, instead of writing "the value of
| i. |
1. (T)—[or]( 2. (T)—[not]( 3. T = maximum( 4. F = 5. (T)—( |
Hypothesis Hypothesis 1, disj. prop. evaluation 2, neg. prop. evaluation 3, 4, ranking |
| ii. |
1. (T)—[if]( 2. (T)—[not]( 3. T = maximum(inverse( 4. F = |
Hypothesis Hypothesis 1, cond. prop. evaluation 2, neg. prop. evaluation |
| ii. |
5. T = inverse( 6. F = 7. (T)—[not]( |
3, 4, ranking 5, inverse funct. 6, neg. prop. evaluation |
| iii. |
1. (T)—[if]( 2. (T)—[if]( 3. T = maximum(inverse( 4. T = maximum(inverse( 5. F = 6. F = 7. F = 8. T = maximum(inverse( 9. (T)—[if]( |
Hypothesis Hypothesis 1, cond. prop. evaluation 2, cond. prop. evaluation 3, def. max., inverse funct. 4, def. max., inverse funct. 5, 6, disjunctive reasoning 7, def. max., inverse funct. 8, cond. prop. evaluation |
| iv. |
1. (T)—[not][not]( 2. (F)—[not]( 3. (T)—( |
Hypothesis, one of the sides 1 = 2, neg. prop. evaluation 2 = 3, neg. prop. evaluation |
| v. |
1. (T)—[not][and]( 2. (F)—[and]( 3. F = minimum( 4. F = 5. T = [not]( 6. T = maximum([not]( 7. (T)—[or][not]( |
Hypothesis, one of the sides 1 = 2, neg. prop. evaluation 2 = 3, conj. prop. evaluation 3 = 4, def. minimum 4 = 5, neg. prop. evaluation 5 = 6, def. maximum 6 = 7, disj. prop. evaluation |
Group 4. Conformity with logical tautologies. We have in mind such laws as:
Each of these propositional forms is by itself a law of logic, in the sense that any proposition that has one of those forms must have the value T, regardless of the content of the proposition. One can easily understand that propositions that have these patterns are true because they have these patterns. And the significant fact about those patterns is that they are constructed exclusively out of the propositional operators [not], [and], [or], [if].
• either P or not P
• if both P and Q then P
• not both P and not P
(T)—[or]-( P)-[not](P)
(T)—[if]-([and](P)(Q))-(P)
(T)—[not]-[and]-(P)-[not](P)
We will show that the nodal configurations that correspond to these logical tautologies are system-tautologies, in the sense that the system can only assign the value T to such propositional configurations. Let's consider the tautology,
If both P and Q then PThe configuration for this propositional form has the two components (P) and (Q). If one considers only the cases in which (P) and (Q) have the values T or F, then these two components produce only the four possible cases displayed below in the columns labeled [1] and [2]:
| T | T | T | T | T | |
| T | F | T | F | T | |
| T | F | F | T | F | |
| T | F | F | F | F |
| [5] | [3] | [1] | [2] | [4] |
The values in columns [1] and [2] produce the values in column [3], using the rule for conjunctions, and column [4] repeats column [1], since they involve the same proposition. The values in columns [3] and [4] then produce the values in column [5], using the rule for conditionals, so that the final value in these four cases is always T.
But there are other cases to consider as well. (P) and (Q) can be propositions that have the value N. In particular, (P) and (Q) can both be N, or just (P) is N, or just (Q) is N:
| N | N | ||||
| N | T | ||||
| N | F | ||||
| T | N | ||||
| F | N |
Since in these five cases the compound proposition involves the value N, the system uses the resolution method to calculate the values of these cases by replacing the values N by the values T and F. But all these scenarios are identical to the four cases above when no value N is involved, and in those cases the final value is always T. This shows then that the propositional compound is a system-tautology, because the system can only assign the value T to this construction.
In the course of this demonstration we have also proven a more general result, that we may call The Resolution Theorem:
An immediate result of this theorem is that the test for being a system-tautology is that all two-valued substitutions produce a final value of T. And, since our rules for evaluating compound propositions when limited to the two-valued case are also the rules used for standard logic, it follows that there is a complete agreement between being a system-tautology and a tautology of standard logic.
§30. Experimental Results. This section is not available.
§31. Conclusion of this paper. This section is not available.
1. We neither assume, as is commonly done, nor do we reject, as do the now so called mysterians, such as McGinn, that explanations can be given for the resultant cognitive representations, in particular, our conscious awareness of qualitative features, solely in terms of the recognized parameters of neuro-biochemistry. A certain neutrality here seems appropriate. On this issue, see Collin McGinn, The Problem of Consciousness, Oxford Univ. Press, 1991, and The Character of Mind, Oxford Univ. Press,1997.
2. Recent discussions of neural networks in connectionist theories invite us to picture a concept as being a neural node with a number of connected neural nodes. But notice that a neural node is likely to be organized sets of neurons that behave as one unit. While our account has a number of similarities with connectionist theories, our shared use of the term "node" should not be construed as an endorsement of such theories. We use the term primarily in its original, abstract, mathematical sense. As will become apparent, our views on several important issues are not consistent with connectionist versions. For example, we propose that (1) some cognitive nodes have sensory content, (2) some have conceptual content and definitions, (3) some are syntactical operators, (4) some possess propositional content and form part of a nodal language of thought. For an exposition of connectionist theory, see D.Rummelhart, J. McClelland, and the PDP Research Group, Parallel Distributed Processing, vols. 1 and 2, MIT Press, 1988. But also see Connections and Symbols, ed. S. Pinker and J. Mehler, MIT Press, 1988, for a critique of connectionist theory.
3. In Hameroff and Penrose, "Conscious events as orchestrated space-time selections," in Explaining Consciousness, The Hard Problem, ed. J. Shear. MIT Press, 1998, Roger Penrose points to various studies by S. R. Hameroff, S. Rasmussen, J. Tuszynski, and B. Libet that show that tubulin proteins inside neurons are capable of representing, propagating, and processing information at the molecular level. This situation is then one possible mechanism for the idea that neural nodes can store the permanent information required for resonant activation. Other possible mechanisms may invoke the special arrangement that neurons have within a neural node.
4. We are familiar with analogous examples of this. The different sound waves generated by the different instruments of an orchestra combine into a single complex sound wave that strikes the eardrums as we listen to the orchestra. But the brain somehow decomposes that complex wave pattern into its original parts, so that we can hear the various individual instruments play as they do by themselves.
5. See chapter 2, "A General Framework for Parallel Distributed Processing," in D. Rummelhart, J. McClelland, and the PDP Research Group, Parallel Distributed Processing, vol. 1, MIT Press, 1988.
6. A note about the relation of types and tokens. From our perspective, types are the permanent cognitive structures of the mind, and tokens are brought about by the activations of such structures. When someone thinks, a type is betokened, that is, a specific representation is brought about by the activation of a structure. Two tokens belong to the same type if they are each brought about by an activation of that type.
7. Note that epiphenomenalism is incompatible with our view that some causal activation relations are resonance activations caused by the activations patterns of cognitive structures. On our view our active thoughts have a causal effect on our thoughts and actions.
8. Daniel Dennett, Consciousness Explained, Little Brown & Co., 1991, chapter 5.
9. Jerry A. Fodor, The Modularity of Mind, MIT Press, 1983
10. See for example, [--references--].
11. It can be proposed that instead of postulating the existence individuative pointer nodes it is sufficient to postulate merely the existence of special reference activation wave patterns by which the activation patterns of our concepts are modified, since it these modifiers that play the explanatory role in our theory of active thoughts. This proposal has real merit, but what leads us to postulate pointer nodes is that the theory also needs a way of explaining how reference activation patterns themselves are generated. We are, of course, open to adequate alternative proposals.
11A. See for example, [--references--].
12. See, David Marr, Vision, W.H.Freeman & Co., 1982; and, F. Crick and C. Koch, "Why Neuroscience May Be Able to Explain Consciousness," Scientific American, 273 (6), December 1995, pp.84-85.
13. Baars, A Cognitive Theory of Consciousness, Cambridge Univ. Press, 1988.
14. Such is Fodor's account of the universal innateness of all simple concepts. For his version of the Nativism vs. Empiricism debate, see Fodor, Representations, Part iv.
14b. See for example, [--references--].
15. Since sensory qualities typically form a continuum, it is plausible that sensory feature units each encode a range of such qualities. Someone's simple conceptual representation (red) would thus be connected in memory with a range of color intensities {color#i}-{color#j}, and (light red) with a certain lower subrange {color#i}-{color#j*}, and (color) with the array of color intensities {color#min}-{color#max}.
16. Here and throughout, labels such as "(apple-shaped)," or "(red)," are arbitrary labels used to refer to neural nodes. We could have used labels such as "node 5731" instead. We use the given labels as a heuristic device to suggest to the reader which neural nodes are being referred to in our discussion. The cognitive system, of course, accesses neural nodes directly through their content.
17. Fodor, "The Present Status of the Innateness Controversy," in Representations, MIT, 1981. Fodor also concludes that, since all simple concepts are innate, all concepts whatsoever are innate. An undesirable result, indeed. On the other hand, by distinguishing between concepts that are part of one's working conceptual repertoire, "triggered" in Fodor's sense, and those that are not, this theory achieves experimental consistency.
18. Hume, A Treatise of Human Nature, Book I, Part I; and Berkeley, Principles of Human Knowledge, "Introduction."
19. See, David Marr, Vision, W.H.Freeman & Co., 1982; and, F. Crick and C. Koch, "Why Neuroscience May Be Able to Explain Consciousness," Scientific American, 273 (6), December 1995, pp.84-85.
20. Cf. Locke, An Essay Concerning Human Understanding, Book III, chapter 1 ff.
21. And yet, we are aware of some sound qualities, as we recognize different speakers, for example. Such perception is better attributed to other sound recognition processes that act in parallel with the given one.
22. It should be noted that the production of a word representation for a word utterance often depends on the simultaneous production of other word representations for the accompanying word utterances. For example, the phrase "I paddled the bay before us" could lead to the representation {"I"} {"paddled"} {"the"} {"baby"} {"for"} {"us"}. (This example was provided by J.D. Trout.) Both syntactic patterns and semantic content each have their influence in the determination of word representations. It is here that Dennett's multiple draft theory of thought is especially appropriate.
22a. The focus on qualia makes all the difference. Compare this account to Frank Jackson's account in his articles "Epiphenomenal Qualia," The Philosophical Quarterly, 32, pp. 127-136, and "What Mary didn't Know," The Journal of Philosophy LXXXIII, 5 (May 1986), pp. 291-295.
22b. This point is a common theme in the history of philosophy. Descartes makes this point explicitly in his comments on article XIII in his Notes directed against a certain Programme, and this theme is the basis of Kant's Critique of Pure Reason.
23. The fact that concepts are only relay nodes may explain the abstract nature that we attribute to our concepts.
24. A little reflection shows that our thoughts employ no undenominated quasi-concepts, or very few of them, since in the absence of public use of words, there would be no circumstances that would result in their formation.
24a. See [--references--].
24b. We owe this view of meaning to Wittgenstein, who in his Philosophical Investigations proposes that the meaning of a word is the set of varying rules we have for employing the word, rules that have no more in common than mere family resemblance.
25. Of course, the blatant assertion "this cat is a tree" will cause the thoughts (cat) and (tree) to be propositionally adjoined, for a while, in the proposition (this cat)(is)(tree), and that thought will result in the consequent judgment: [false](this cat)(is)(tree).
26. Quine, "Two Dogmas of Empiricism," and "Meaning in Linguistics," From a Logical Point of View, Harvard University Press, 2nd ed., 1961.
27. Old concepts never go away. They tag along with the new ones, usually under the same name. And that is why we, who have the new concepts, can always understand people who employ the old concepts, because we have and use the old ones too.
28. The automatic introduction of conceptual representations through adjunction should not be confused with the different mental activities of making judgments or forming beliefs. When visually confronted with an apple, we will think the concept (apple) and as well as the proposition (that is an apple). Still, we may come to reject that proposition, and accept the proposition (that is made of wax) instead.
29. We do not here enter into the debate about whether iconic representations, like qualia, do in fact exist. We assume that they do. For some details on this debate see the articles by Pylyshyn, Kosslyn, Fodor, Dennett, and others, in Readings in Philosophy of Psychology, vol. 2, ed. Ned Block, Harvard Univ. Press, 1991, and Imagery, ed. Ned Block, MIT Press, 1982.
30. There is an analogy. Both visual and auditory information is electronically stored on recording media such as VCR tapes and CDs.
32. See for example, Fodor, Representations, Chapter 10.
33. The notation [is] is not significant. Our only purpose is to indicate the operation of predication, and alternative notation such as [>] could serve as well.
34. We leave it an open question how the kinds of formal conceptual structures we have presented here are related to the grammatical patterns of the transformational grammars introduced by Chomsky and others. See, Noam Chomsky, Aspects of the Theory of Syntax, MIT Press, 1965, and Syntactic Structures, Mouton & Co., 1966.
35. Beginning in the early 70's and extending to the present, Jerry Fodor has been a strong and prolific proponent of a language of thought. See his [--references--]. However, Fodor has not discovered what such a language is actually like, and he has been skeptical about the possibility of such a discovery.
36. For example, all the various systems of modal logic, relevance logic, intuitionistic logic, deviant logic, fuzzy logic, deontic logic, and so forth. Non-truth-functionality is the norm in non-standard logics. See, [--references--].
All contents copyright © 9/2000, 5/2003, 1/2008, 1/2009 Arnold vander Nat, all rights reserved.
Department of Philosophy
Loyola University Chicago.